Finding a set of line segments to fit noisy data

Question

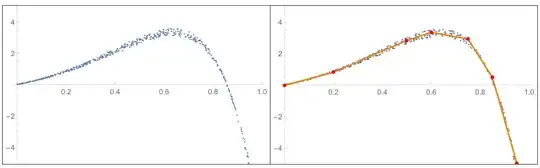
Looking for a methodology to choose line segments that are a rough fit to a given set of data. In this example, the data are {x,y} pairs. For example, if the data looked like what is shown on the left, then would like to find a few line segments that go through the data, as shown on the right.

For this application

line segments are required – curves will not work with other parts of the system
line segments are continuous, so that the end of one line segment is the beginning of the next.
the number of line segments is arbitrary – chosen either by the user or by an improved algorithm

A methodology that works is shown below. Any recommendations for other methods that might be more general or more efficient would be appreciated.

The methodology below uses FixedPoint and FindMinimum. At the inner level, it uses FindMinimum to determine new y-values for pairs of points, starting with the points 1 and 2, proceeding to points 2 and 3, and ending with points n-1 and n. At the outer level, the methodology below uses FixedPoint to repeat this process or stop after the maximum number of iterations is reached. The methodology below pushes the following responsibilities to the user:

number of points to use for the line segments
x-value for each point
range of x and y values (though this could easily be automated)

Seeking suggestions about other approaches or improvements to what is shown below. Thanks!

(*problem definition*)
ptsData = {N@#, 
     N@((-3.5 #^2 + 3 #) Exp[3 #] ) (1 + 
        RandomReal[{-0.075, +0.075}])} & /@  RandomReal[{0, 1}, 500];
xyStart = {#, 0} & /@ {0, 0.2, 0.5, 0.6, 0.75, 0.85, 0.95, 1.0};
xRange = {0, 1};
yRange = {-20, 10};
(*analysis*)
xyNew = findNewYvaluesFromData[ptsData, xRange, yRange, xyStart, 10]
(*results*)
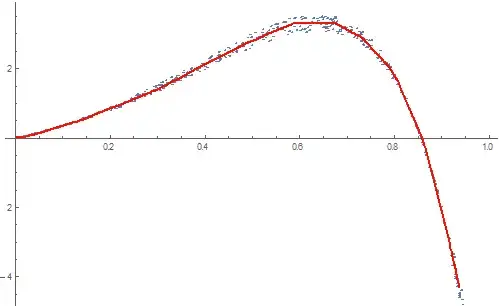
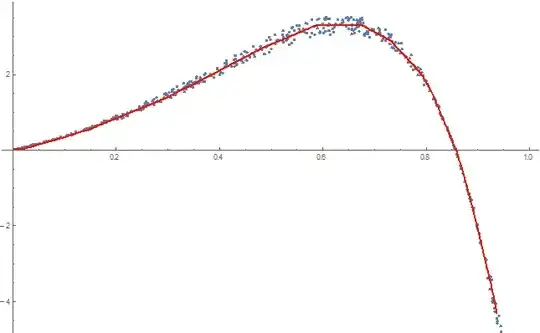
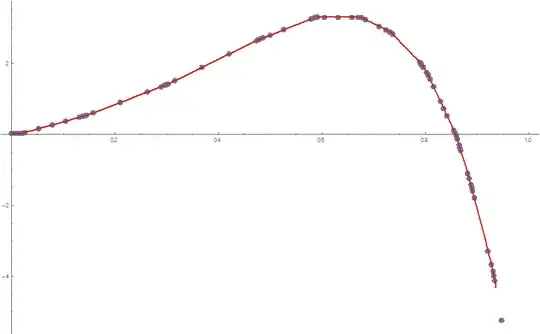
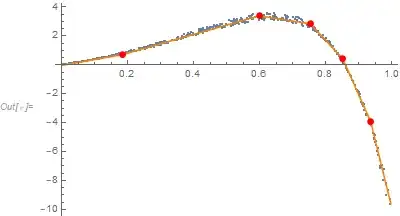
ListPlot[ ptsData, PlotRange -> { Automatic, {-5, 5} }, 
 Epilog -> {Orange, AbsoluteThickness[2], AbsolutePointSize[5], 
   Line[xyNew] , Red, Point[xyNew]}]

And below is the methodology implemented thus far

Clear[findNewYvaluesFromData]
(*repeatdly improve y values in the list xyIn, until convergence or \
maximum number of iterations, nIts*)
findNewYvaluesFromData[
  xyData_, {xminIn_, xmaxIn_}, {yminIn_, ymaxIn_}, xyIn_, nIts_] := 
 FixedPoint[ 
  findNewYvaluesFromData[
    xyData, {xminIn, xmaxIn}, {yminIn, ymaxIn}, #] &, xyIn, nIts]
(improve y values in the list xyIn, by minimizing the deviation 

between xyData and a linear interpolation of the list xyIn)
findNewYvaluesFromData[
  xyData_, {xminIn_, xmaxIn_}, {yminIn_, ymaxIn_}, xyIn_] := 
 Fold[update2YvaluesFromData[
    xyData, {xminIn, xmaxIn}, {yminIn, ymaxIn},  #1, #2 ] &, xyIn,

  makePairsij[Range@Length@xyIn] ]
Clear[update2YvaluesFromData]
(improve y values at postions i,j in the list xyIn  )
(y values are improved by comparing a linear interpolation of the 

list xyIn with xyData )
(FindMinimum is used to determine the improved y values.)
update2YvaluesFromData[
  xyData_, {xminIn_, xmaxIn_}, {yminIn_, ymaxIn_}, xyIn_, {i_, j_}] := 
 Module[{xyNew, r, yi, yj},
  r = FindMinimum[
    avgErr2YvaluesFromData[xyData, {xminIn, xmaxIn}, xyIn, {i, j}, 
     yi, yj], {yi, xyIn[[i, 2]], yminIn, ymaxIn}, {yj, xyIn[[j, 2]], 
     yminIn, ymaxIn}, AccuracyGoal -> 2 , PrecisionGoal -> 2];
xyNew = xyIn;
  xyNew[[i, 2]] = yi /. r[[2]];
  xyNew[[j, 2]] = yj /. r[[2]];
  xyNew
  ]
Clear[avgErr2YvaluesFromData]
(compare xyData with a linear interpolation function  over the range 

[xmin, xmax] )
(linear interpolation function uses xyIn with y values replaced at 

positions i and j )
avgErr2YvaluesFromData[xyData_, {xminIn_, xmaxIn_}, xyIn_, {i_, j_}, 
  yi_?NumericQ, yj_?NumericQ] := Module[{xyNew, fLin, sum, x},
  xyNew = xyPairsUpdate[xyIn,  {xminIn, xmaxIn}, {i, j}, yi, yj];
  fLin = Interpolation[xyNew, InterpolationOrder -> 1];
  Fold[#1 + Abs[Last@#2 - fLin[First@#2 ] ] &, 0, xyData]  / 
   Max[1, Length@ xyData]
  ]
Clear[makePairsij]
(choose adjacent pairs from a list )
(makePairsij[list_] := {list[[#]], list[[#+1]]} & /@ 

Range[Length@list - 1])
makePairsij[list_] := 
 ListConvolve[{1, 1}, list, {-1, 1}, {}, #2 &, List]
Clear[xyPairsUpdate]
(prepare xyV list for Interpolation function)
(1) ensure that there is a point at xmin and xmax)
(2) remove duplicates)
xyPairsUpdate[xyV_, {xminIn_, xmaxIn_}, {i_, j_}, yi_, yj_] := 
 Module[{xyNew},
  (to do: remove duplicate values)
  xyNew = Sort[xyV];
  xyNew = DeleteDuplicates[xyNew, Abs[First@#1 - First@#2] < 0.0001 &];
  xyNew[[i, 2]] = yi;
  xyNew[[j, 2]] = yj;
  xyNew = 
   If[xminIn < xyNew[[1, 1]], 
    Prepend[xyNew, {xminIn, xyNew[[1, 2]]}], xyNew];
  xyNew = 
   If[xmaxIn > xyNew[[-1, 1]], 
    Append[xyNew, {xmaxIn, xyNew[[-1, 2]]}], xyNew];
  xyNew
  ]
Clear[xyPairsCheck]
(prepare xyV list for Interpolation function)
(1) ensure that there is a point at xmin and xmax)
(2) remove duplicates)
xyPairsCheck[xyV_, {xminIn_, xmaxIn_}, {i_, j_}] := Module[{xyNew},
  (to do: remove duplicate values)
  xyNew = Sort[xyV];
  xyNew = DeleteDuplicates[xyNew, Abs[First@#1 - First@#2] < 0.0001 &];
  xyNew
  ]

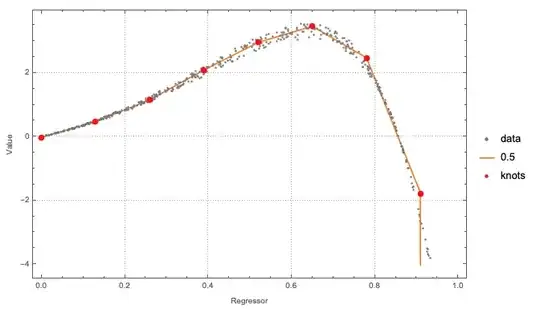
It's very easy to get piecewise linear fits like this by training a neural network with Ramp nonlinearities. See the first example in this blog post. — Sjoerd Smit, Oct 02 '20 at 15:47
@SjoerdSmit "It's very easy to get piecewise linear fits by training a neural network with Ramp nonlinearities." Elegant? Yes. Appropriate? Yes. Should be done more? Yes. Easy? No way. Easy to explain to someone else without an expert handy? I don't think so. — JimB, Oct 02 '20 at 17:17
Your figure seems to indicate that you need the starting and ending points to be data points. Is that the case? I ask because the "usual" (but not required) approach is to use $n-1$ breakpoints to obtain $n$ segments. — JimB, Oct 02 '20 at 17:28
You could use the simple method I developed here. Set the interpolation function to first order to get a piecewise linear fit. — Hugh, Oct 02 '20 at 17:48
@JimB I would say it's easy in terms of the code you need to write. The example I cited is just a few lines and none of it is particularly obtuse. — Sjoerd Smit, Oct 02 '20 at 18:34
Of course I'm only referring to the standard training methodology here (which should be sufficient for this problem), not to the rest of the blog post. — Sjoerd Smit, Oct 02 '20 at 18:41
@JimB For this question, the starting and end points of the line segments do not need to exactly match a data point. — user6546, Oct 02 '20 at 18:55

score 10 · Answer 1 · answered Oct 02 '20 at 18:56

To illustrate my comment, here is a minimal example:

ptsData = {N@#, N@((-3.5 #^2 + 3 #) Exp[3 #]) (1 + RandomReal[{-0.075, +0.075}])} & /@ RandomReal[{0, 1}, 500];
net = NetTrain[
  NetChain[{20, Ramp, 20, Ramp, 1}],
  Rule @@@ ptsData
 ];
Show[
 ListPlot[ptsData],
 Plot[net[x], {x, 0, 1}, PlotStyle -> Red]
];

The model produced by the network is piecewise linear because of the Ramp non-linearities. In principle you could extract the matrices from the network to figure out where exactly the knot points of the function are, but that would be quite a bit more work. If you're only interested in the piecewise function itself, though, this is probably the easiest way to get one.

The network can also be used with FunctionInterpolation to generate a first order interpolation function:

int = Quiet @ FunctionInterpolation[net[x], {x, 0, 1}, InterpolationOrder -> 1, 
    InterpolationPoints -> 20
];
Show[
 ListPlot[ptsData],
 Plot[int[x], {x, 0, 1}, PlotStyle -> Red]
]

With some tinkering, you can extract the knot points from the interpolation function object:

Show[
 ListPlot[Transpose[Flatten /@ (List @@ int[[{3, 4}]])]],
 Plot[int[x], {x, 0, 1}, PlotStyle -> Red]
]

Thanks! that makes it very clear. As pointed out in the previous comments, this should an option considered for similar problems. Thanks for posting the example. — user6546, Oct 04 '20 at 14:45

score 6 · Accepted Answer · answered Oct 02 '20 at 17:26

Here's a brute force Frequentist approach. It does not account for heterogeneity of variance as can the approach described by @SjoerdSmit.

* Generate data *)
ptsData = {N@#, N@((-3.5 #^2 + 3 #) Exp[3 #]) (1 + RandomReal[{-0.075, +0.075}])} & /@ RandomReal[{0, 1}, 500];
(* Number of segments *)
nSegments = 6
(* Segment bounds )
bounds = {-∞, Table[c[i], {i, nSegments - 1}], ∞} // Flatten
( {-∞, c[1], c[2], c[3], c[4], c[5], ∞} *)
(* All intercepts are functions of the initial intercept and the slopes and segment bounds )
( This makes the segments continuous *)
Do[intercept[i] = intercept[i - 1] + c[i - 1] (slope[i - 1] - slope[i]), {i, 2, nSegments}]
(* Define model *)
model = Sum[(intercept[i] + slope[i] x) Boole[bounds[[i]] < x <= bounds[[i + 1]]], {i, nSegments}];
(* Determine initial estimates for the bounds and create the restrictions *)
{xmin, xmax} = MinMax[ptsData[[All, 1]]];
parms = Flatten[{intercept[1], Table[slope[i], {i, nSegments}], 
   Table[{c[i], xmin + (xmax - xmin) i/nSegments}, {i, 1, nSegments - 1}]}, 1]
restrictions = Less @@ Join[{xmin}, Table[c[i], {i, nSegments - 1}], {xmax}]
(* Fit model with restrictions *)
nlm = NonlinearModelFit[ptsData, {model, restrictions}, parms, x]
(* Show estimates )
nlm["BestFitParameters"]
( {intercept[1] -> -0.0332834, slope[1] -> 4.05435, slope[2] -> 6.50846,
   slope[3] -> -3.59535, slope[4] -> -24.7879, slope[5] -> -51.4635, 
   slope[6] -> -92.9577, c[1] -> 0.18565, c[2] -> 0.597779, 
   c[3] -> 0.753081, c[4] -> 0.850668, c[5] -> 0.935081} )
nlm["AICc"]
( -711.052 *)

Show results:

Show[ListPlot[ptsData, PlotRange -> All],
 Plot[nlm[x], {x, xmin, xmax}, PlotStyle -> Orange, PlotRange -> All],
 ListPlot[Table[{c[i], nlm[c[i]]} /. nlm["BestFitParameters"], {i, 1, nSegments - 1}],
   PlotStyle -> {{PointSize[0.02], Red}}]]

One might choose the number of segments with the smallest AICc value.

are there some advantages to using the slope[i] as parameters rather than y[i] ? — user6546, Oct 04 '20 at 14:48

Anton Antonov · Answer 3 · 2020-10-03T13:04:31.507

Using WFR's function QuantileRegression:

(* Generate data *)
ptsData = 
  SortBy[{N@#, 
      N@((-3.5 #^2 + 3 #) Exp[3 #]) (1 + 
         RandomReal[{-0.075, +0.075}])} & /@ RandomReal[{0, 1}, 500], 
   First];
(* Quantile regression computation with specified knots *)
knots = Rescale[Range[0, 1, 0.13], MinMax@ptsData[[All, 1]]];
probs = {0.5};
qFuncs = ResourceFunction["QuantileRegression"][ptsData, knots, probs,
    InterpolationOrder -> 1];
(* Plot results *)
ListPlot[
 Join[
  {ptsData},
  (Transpose[{ptsData[[All, 1]], #1 /@ ptsData[[All, 1]]}] &) /@ 
   qFuncs,
  {{#, qFuncs[[1]][#]} & /@ knots}
  ],
 Joined -> Join[{False}, Table[True, Length[probs]], {False}],
 PlotStyle -> {Gray, Orange, {Red, PointSize[0.014]}},
 PlotLegends -> Join[{"data"}, probs, {"knots"}],
 PlotTheme -> "Detailed",
 FrameLabel -> {"Regressor", "Value"},
 ImageSize -> Large]

The knots specification can be just an integer. I used a list of x-coordinates in order to show that custom knots can be specified.

@user6546 Welcome! And, yes, using QR is much better for your problem than the approaches in the other two answers. :) — Anton Antonov, Oct 04 '20 at 15:34

Finding a set of line segments to fit noisy data

3 Answers3