RootSearch warning "too small to represent as a normalized machine number"

Question

RootSearch is a package for finding all roots within a range from Ted Ersek. As I test it, it is quite robust. But I also encountered some issue that I can not resolve.

I define a function

ClearAll[f];
f[r_?NumericQ] := 
 Sort[Re@Eigenvalues[{{3.5` - 1.6` Cos[Im[E^(I 0.) r]] - 
        2.4` Cos[Re[E^(I 0.) r]], 0, -0.07`, 0}, {0, 
       3.5` - 2.4` Cos[Im[E^(I 0.) r]] - 1.6` Cos[Re[E^(I 0.) r]], 
       0, -0.07`}, {-0.07`, 
       0, -3.5` + 1.6` Cos[Im[E^(I 0.) r]] + 2.4` Cos[Re[E^(I 0.) r]],
        0}, {0, -0.07`, 
       0, -3.5` + 2.4` Cos[Im[E^(I 0.) r]] + 
        1.6` Cos[Re[E^(I 0.) r]]}}]][[3]]

the plot is quite usual

Now I want to find points where the first derivative of f are zero using RootSearch.

If I do it as

roots = RootSearch[f'[t] == 0, {t, 0., 1.}];

there will be a warning

General::munfl: 2.2204510^-16 2.2250710^-308 is too small to represent as a normalized machine number; precision may be lost.

And no result came out after I waited for several minutes.

However, If I do

roots = RootSearch[f'[t] == 0.0001, {t, 0., 1.}];

It finishes in seconds.

and

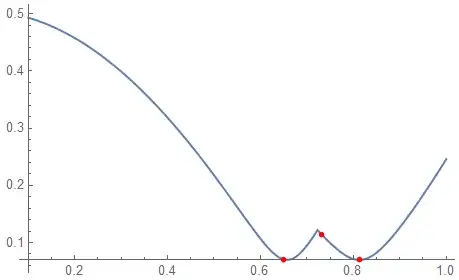
vals = Table[{i, f[i]}, {i, Flatten[roots][[;; , -1]]}];
Plot[f[x], {x, 0.1, 1}, PlotRange -> All, 
 Epilog -> {PointSize[Medium], Red, Point[vals]}]

shows

So, why is RootSearch[f'[t] == 0, {t, 0., 1.}] not working?

I also find as simple as RootSearch[Sin[x] == 0, {x, 0, 100}] will also gives precision lost warning, but it gives result immediately.

PS:

I found that if I change the interval to {0.1,1} then

RootSearch[f'[t] == 0, {t, 0.1, 1.}]

will work. So it is t=0 cause the problem. Why is that?

another much simple case I just found is

ClearAll[g];
g[x_?NumericQ]:=x^3;

and

RootSearch[g'[x] == 0, {x, -1, 1}]

will not give an answer. But

RootSearch[3x^2 == 0, {x, -1, 1}]

gives answer immediately.

This is a valuable case, because Plot based root finding or NDSolve event locating method can not deal with this case( first derivative only touch x axis, not penetrating it)

Answer 1

RootSearch is an old program and changes in Mathematica since my last update cause RootSearch to have problems when looking for a root of f[x] near x=0. There is a function Ulp2[x1,x2] in the package that determines how far it is from x1 to the nearest approximate number towards x2. Ulp2 gets hung up when x1 is machine precision zero. I might put an updated version on the Wolfram Function Repository in the coming weeks. Your problem can be simplified considerably. Change 0.0 to integer zero. Then for real r:

Im[E^(I*0)*r]->0
Re[E^(I*0)*r]->r

So your problem simplifies to:

Eigenvalues[{
{35 - 16 - 24*Cos[r], 0, -7/10, 0},
{0, 35 - 24 - 16*Cos[r], 0, -7/10},
{-7/10, 0, -35 + 16 + 24*Cos[r], 0},
{0, -7/10, 0, -35 + 24 + 16*Cos[r]}}/10]

$\left\{-\frac{1}{100} \sqrt{-35200 \cos (r)+12800 \cos (2 r)+24949},\frac{1}{100} \sqrt{-35200 \cos (r)+12800 \cos (2 r)+24949},-\frac{1}{100} \sqrt{-91200 \cos (r)+28800 \cos (2 r)+64949},\frac{1}{100} \sqrt{-91200 \cos (r)+28800 \cos (2 r)+64949}\right\}$

The output of NMinimize below shows that for any real r, you are taking the square root of a positive number in the above.

N@Minimize[24949-35200 Cos[r]+12800 Cos[2 r],Element[r,Reals]]
N@Minimize[64949-91200 Cos[r]+28800 Cos[2 r],Element[r,Reals]]

You will always have two positive and two negative eigen-values. Next I find r where one of the positive eigen-values becomes greater than the other positive eigen-value.

FindRoot[24949-35200 Cos[r]+12800 Cos[2 r]==64949-91200 Cos[r]+28800 Cos[2 r],{r,0.7}]

(* Out[]= {r->0.722734} *)

The following f[r_] gives the same result as yours, but it provides much more insight into your problem.

Clear[f]
f[r_]:=Piecewise[{
  {Sqrt[ 64949-91200 Cos[r]+28800 Cos[2 r]]/100,r<0.7227342478134149},
  {Sqrt[24949-35200 Cos[r]+12800 Cos[2 r]]/100,0.7227342478134149<=r}
 }];
 Plot[f[x],{x,0,1}]