How can I draw a sphere in the Minkowski space?

Question

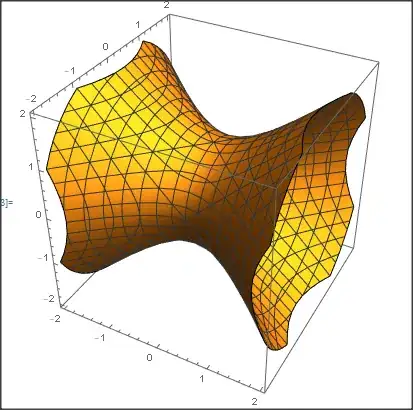
If the equation of the circle in the Minkowski 3 space is given as
$S_1^2 = \{x \in E_1^3:- x_1^2 + x_2^2 + x_3^2 \}$, how can I replace it in the following code?

f[u_] :=
 (eqns = {t'[s] == κ[s] n[s], 
    n'[s] == -κ[s] t[s] + τ[s] b[s], 
    b'[s] == -τ[s] n[s], r'[s] == t[s], t[0] == t0, n[0] == n0, 
    b[0] == b0, r[0] == r0};
  Subscript[v, x0] = u;
  α = .4; β = 0.5;
  κ[s_] = 2 β Sech[u α + s β];
  τ[s_] = 1 - α/β;
  {t0, n0, b0} = Orthogonalize[{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}];
  r0 = {0, 0, 0};
  sol = First@NDSolve[eqns, {r, t, n, b}, {s, 0, 20}];
  ParametricPlot3D[Evaluate[r[s] /. sol], {s, 0, 20}, 
   PlotStyle -> {Thick, Red}, PlotRangePadding -> 1, Boxed -> False, 
   Axes -> None
   ])
gm[u_] :=
 (eqns = {t'[s] == κ[s] n[s], 
    n'[s] == -κ[s] t[s] + τ[s] b[s], 
    b'[s] == -τ[s] n[s], r'[s] == t[s], t[0] == t0, n[0] == n0, 
    b[0] == b0, r[0] == r0};
  α = .4; β = 0.5;
  κ[s_] = 2 β Sech[u α + s β];
  τ[s_] = 1 - α/β;
  {t0, n0, b0} = Orthogonalize[{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}];
  r0 = {0, 0, 0};
  sol = First@NDSolve[eqns, {r, t, n, b}, {s, 0, 20}];
  Graphics3D[
   Text[Style["t=" <> ToString[u], Black, Italic, 
     30], {Evaluate[r[20] /. sol]}]])
Show[Table[f[u], {u, 0, 4}], Table[gm[u], {u, 0, 4}], PlotRange -> All]
g1[u_] := (eqns = {t'[s] == κ[s] n[s], 
     n'[s] == -κ[s] t[s] + τ[s] b[s], 
     b'[s] == -τ[s] n[s], r'[s] == t[s], t[0] == t0, n[0] == n0, 
     b[0] == b0, r[0] == r0};
   α = .4; β = 0.5;
   κ[s_] = 2 β Sech[u α + s β];
   τ[s_] = 1 - α/β;
   {t0, n0, b0} = Orthogonalize[{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}];
   r0 = {0, 0, 0};
   sol = First@NDSolve[eqns, {r, t, n, b}, {s, 0, 20}];
   ParametricPlot3D[Evaluate[t[s] /. sol], {s, 0, 20}, 
    PlotStyle -> {Thick, Blue}, PlotRange -> All, Boxed -> False, 
    Axes -> None]);
sph = SphericalPlot3D[{1}, {θ, 0, Pi}, {ϕ, 0, 2 Pi}, 
   Boxed -> False, Axes -> None, 
   PlotStyle -> 
    Directive[Orange, Opacity[0.7], Specularity[White, 10]], 
   Mesh -> None, PlotPoints -> 10];

where in the above code, we draw an evolved curve on a sphere in the Euclidean space. In the Minkowski space (timelike type) we have Frenet formulae as:

$\qquad t' = \kappa\,n,\quad n' = \kappa\,t + \tau\,b, \quad b' = - \tau\,n$.

Also, $<t,\,t>\, = -1$, $<n,\,n>\, = 1$, $<b,b>\, = 1$, $t \times n = b$, $n \times b = - t$ and $b \times t = n$. The inner product is defined as

$\qquad <x,y>\, = - x_{1}\, y_{1} + x_{2}\, y_{2} + x_{3}\, y_{3}$

where

$\qquad x =\, <x_{1},x_{2},x_{3}> \quad y =\, <y_{1} ,y_{2},y_{3}>$.

and the cross product is

$\qquad x \, \times \, y = \begin{vmatrix} -e_{1} & e_{2} & e_{3} \\ x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \end{vmatrix}$.

Can any one help?. I need applying the same code above in the Minkowski space.

Something to adjust since $−x_1^2+x_2^2+x_3^2 $ is not any equation. — user64494, Oct 08 '20 at 13:39

score 10 · Accepted Answer · edited Jun 27 '23 at 22:27

A sphere means all point that have the same distance from the some origin, for simplicity we consider the unit sphere at the origin. The only thing that is different from the usual R^3 is the metric that measures the distance. In this case the distance from the origin is -x^2+y^2+z^2 and not x^2+y^2+z^2. In other words, we are looking for all points with -x^2+y^2+z^2 == 1.

We may use ContourPlot3D to make a picture of the unit sphere with Minkowski metric:

ContourPlot3D[-x^2 + y^2 + z^2 == 1, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

How can I draw a sphere in the Minkowski space?

1 Answers1