6

Consider a set of (here) 3 series


r`data = Thread[{Range@4, # Range@4}] & /@ (10 Range@3);
(*{
{{1, 10}, {2, 20}, {3, 30}, {4, 40}}, 
{{1, 20}, {2, 40}, {3, 60}, {4, 80}},
{{1, 30}, {2, 60}, {3, 90}, {4, 120}}
}*)

The intent is to divide the second coordinate of each point in each series by some divisor divs[[i]]

r`divs = 10 Range@3;
(*{10, 20, 30}*)

I am currently achieving this as follows

r`f[x_] := #/x &
MapThread[MapAt[r`f@#2, #1, {All, 2}] &, {r`data, r`divs}]
(*{
{{1, 1}, {2, 2}, {3, 3}, {4, 4}},
{{1, 1}, {2, 2}, {3, 3}, {4, 4}},
{{1, 1}, {2, 2}, {3, 3}, {4, 4}}
}*)

How to eliminate r`f in favour of directly nesting the division lambda #/x &, present in the MapAt, inside the MapThread?

In other words how to correctly write something of the kind

MapThread[MapAt[#/#2 &, #1, {All, 2}] &, {r`data, r`divs}]
                ^           
                |
                |
      should refer to second coord of point
             and not r`data[[i]]

Please note that I did go through similar questions (e.g. MapThread on a nested Map) but couldn't apply their solutions to the present case.

lineage
  • 1,144
  • 4
  • 10

3 Answers3

7
MapThread[MapAt[z \[Function] z/#2, #1, {All, 2}] &, {r`data, r`divs}]

or

MapThread[MapAt[Function[z, z/#2], #1, {All, 2}] &, {r`data, r`divs}]

or

MapThread[Function[{x, y}, MapAt[#/y &, x, {All, 2}]], {r`data, r`divs}]

{{{1, 1}, {2, 2}, {3, 3}, {4, 4}}, {{1, 1}, {2, 2}, {3, 3}, {4, 4}}, 
{{1, 1}, {2, 2}, {3, 3}, {4, 4}}}

Alternatively,

Transpose[Transpose[#]/{1, #2}] & @@@ Transpose[{r`data, r`divs}]

MapThread[Transpose[Transpose[#]/{1, #2}] &, {rdata, rdivs}]


MapThread[ReplacePart[#, {i_, 2} :> #[[i, 2]]/#2] &, {rdata, rdivs}]


SubsetMap[Flatten[Partition[#, First[Length /@ r`data]]/rdivs] &, rdata, 
  {All, All, 2}]


Module[{z = rdata}, z[[All, All, 2]] = z[[All, All, 2]]/rdivs;z]

all give

{{{1, 1}, {2, 2}, {3, 3}, {4, 4}}, {{1, 1}, {2, 2}, {3, 3}, {4, 4}},
 {{1, 1}, {2, 2}, {3, 3}, {4, 4}}}

And... a Halloween special:

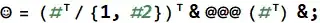
enter image description here

☺[{r`data, r`divs}]

{{{1, 1}, {2, 2}, {3, 3}, {4, 4}}, {{1, 1}, {2, 2}, {3, 3}, {4, 4}}, 
 {{1, 1}, {2, 2}, {3, 3}, {4, 4}}}
kglr
  • 394,356
  • 18
  • 477
  • 896
  • so one can't escape having to define the MapAt's func explicitly? – lineage Oct 09 '20 at 18:08
  • thnx for introducing me to spliced assignment! – lineage Oct 09 '20 at 18:42
  • @lineage, if you have to use MapThread + MapAt combination I don't know how we can avoid defining the function for the first argument of MapAt. If MapAt is not required, Carl's suggestion in the comments is a clean way to get the desired result. – kglr Oct 09 '20 at 18:50
4

By using ReplacePart in place of any mapping function, there is no need to define any function, neither explicitly like your r`f nor as a pure function.

data = Thread[{Range @ 4, # Range @ 4}]& /@ (10 Range @ 3);
divisors = 10 Range @ 3;
ReplacePart[
  data, 
  {i_, j_} :> Module[{m = data[[i, j]]}, m[[2]] = m[[2]]/divisors[[i]]; m]]

{{{1, 1}, {2, 2}, {3, 3}, {4, 4}}, 
 {{1, 1}, {2, 2}, {3, 3}, {4, 4}}, 
 {{1, 1}, {2, 2}, {3, 3}, {4, 4}}}
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
3

In Mathematica version 12.1+ we can use OperatorApplied to inject the outer argument into the inner function:

MapThread[MapAt[OperatorApplied[#/#2&][#2], #1, {All, 2}] &, {r`data, r`divs}]

(*
{{1, 1}, {2, 2}, {3, 3}, {4, 4}},
{{1, 1}, {2, 2}, {3, 3}, {4, 4}},
{{1, 1}, {2, 2}, {3, 3}, {4, 4}}
*)

Curry from version 11.3+ does the same thing but is now considered obsolete. For more details on these and related constructions, see (197168).

WReach
  • 68,832
  • 4
  • 164
  • 269