Is there something akin to "SubgraphIsomorphismQ" in Mathematica 9?

Question

Provided two unlabeled graphs, $G$ and $H$, I would like to test where $H$ is a subgraph of $G$. In other words, I'd like to test whether we can prune some fixed number of vertices or edges from $G$ to transform it into the graph $H$.

Is there an implementation for something like this in Mathematica 9, or perhaps available elsewhere? Efficiency, within reason, doesn't matter too much to me.

NOTE - I can somewhat tolerate false-positives, but no false negatives.

Is your question "Does MMA have a built-in implementation of UnlabeledSubgraphQ?" or "How can I implement such a function?" If it is the latter, then you'll need to show some original effort. — VF1, Apr 14 '13 at 04:12
@VF1 My original question was: "Does MMA 9 have an implementation? The answer is no. I'm now asking for outside implementations, not for someone to implement an algorithm from the literature. There are multiple non-trivial to implement solutions in the literature. — PinoAir, Apr 14 '13 at 04:40

score 9 · Answer 1 · edited Feb 05 '18 at 19:02

I'll first introduce an auxiliary function, FindSubgraph, that I will use to define the function SubgraphIsomorphismQ the OP asks for. It finds the shortest subgraph of the main graph that is isoporphic to a graph you specify.

This is the second version of this function. This one is slower, but repairs a problem with my original concept. The description of the older version (provided below) remains mostly valid, apart from the part about sorting.

The function basically sets up a matching pattern for the anonymous edges in the edge list of the subgraph that is to be found. The reason they are 'anonymous' is that we are looking for 'unlabeled' graphs (note that the original question didn't have this requirement; an answer to that question is given at the very bottom of this post).

Interesting in the implementation is that I used two layers of abstract labeling of the pattern. First we have anonymous labeling of the vertex pairs in a pattern, and this pattern is anonymously labeled as well to be able to refer to the results of the match. I also used an (undefined) function with the Orderless attribute to force Mathematica to try to find matching edges in any possible order.

ClearAll[FindSubgraph];

FindSubgraph[big_?UndirectedGraphQ, small_?UndirectedGraphQ] :=
 Module[{vl = VertexList[small], 
         el = EdgeList[small] /. UndirectedEdge[ a_, b_] :> UndirectedEdge[a,b] | UndirectedEdge[b,a], 
         v, pv, e, pe, f},
  SetAttributes[f, Orderless];
  v = Table[Unique[], {Length@vl}];
  pv = Pattern[#, _] & /@ v;
  e = Table[Unique[], {Length@el}];
  f @@ EdgeList[big] /.
   (f @@ Riffle[MapThread[Pattern, {e, el}] /. Thread[vl -> pv], ___, {1, -1, 2}]) -> e
 ]

Note that the use of Riffle here is merely a remnant of my previous version. However, I kept it this way as it is also a convenient way to insert the maximum number of ___ patterns that may be necessary. Due to the Orderless function, riffling the ___ isn't necessary anymore (but it doesn't do harm either).

This following two tests were reasonably fast:

bmg = GraphData["BrinkmannGraph"];

HighlightGraph[bmg, 
   FindSubgraph[
     bmg, 
     Graph[{1 <-> 2, 2 <-> 3, 3 <-> 4, 4 <-> 5, 5 <-> 6, 6 <-> 7, 7 <-> 1}]
   ]
]

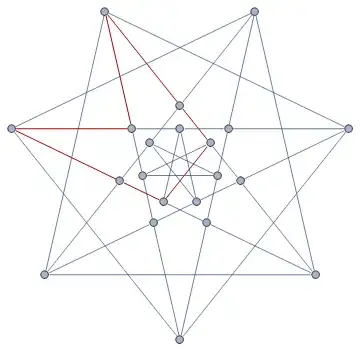
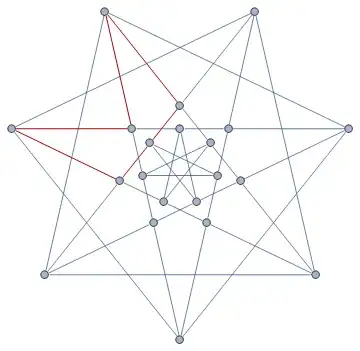
enter image description here

HighlightGraph[bmg, 
  FindSubgraph[
    bmg, 
    Graph[{"ape" <-> "nut", "nut" <-> "mouse", "mouse" <-> "dad", 
           "dad" <-> "sheep", "sheep" <-> "goat", "goat" <-> "ape"}
    ]
  ]
]

enter image description here

but this one took like 20 minutes:

fg = GraphData[{"Fullerene", {26, 1}}];

HighlightGraph[fg, 
   FindSubgraph[
     fg, 
     Graph[{1 <-> 2, 2 <-> 3, 3 <-> 4, 4 <-> 5, 5 <-> 6, 6 <-> 7, 7 <-> 8, 8 <-> 1}]
   ]
]

enter image description here

Older version

I'll first introduce a function that tries to find the shortest subgraph of a graph that contains all the edges of a given second graph (in isomorphical sense). I take it for given that the graphs are undirected (I could use UndirectedGraph to make sure they are).

ClearAll[FindSubgraph];
FindSubgraph[big_?UndirectedGraphQ, small_?UndirectedGraphQ] :=
 Module[{vl = VertexList[small], el = EdgeList[small], v, pv, e, pe},
  v = Table[Unique[], {Length@vl}];
  pv = Pattern[#, _] & /@ v;
  e = Table[Unique[], {Length@el}];
  Graph[
   Sort[Sort /@ EdgeList[big]] /.
    Riffle[
      MapThread[Pattern, {e, Sort[Sort /@ el]}] /. Thread[vl -> pv],
      ___, 
      {1, -1, 2}
    ] -> e
  ]
]

It's a bit (too?) complicated, so I'll explain a bit what's going on here.

Fist step is sorting all the edge lists in canonical order. I sort both the edges and the vertices making up the edges. Since we have undirected graphs, this doesn't change the graphs in principle. The reason for this is to prepare for pattern matching.

Second step is converting each edge in the small graph into a pattern of the form $100:_$50<->$51. All the vertices are replaced by a unique pattern (like $50<->$51, the /.Thread[vl -> pv]) does that). This takes care of the 'unlabeling' of the graph (makes it independent of the actual names of the vertices). The MapThread[Pattern part takes care of naming this pattern.

Riffle is used to generate the final pattern by mixing in BlankNullSequence (___). The end result is a pattern like {___,$100:_$50<->$51,___,$101:_$51<->$52,___}

What follows is a simple replacement with /.. By default, Mathematica tries to find the shortest match and the replacement returns the corresponding edges in the big graph as a Graph.

Test

bmg = GraphData["BrinkmannGraph"];

HighlightGraph[bmg, 
    FindSubgraph[
      bmg, 
      Graph[{1 <-> 2, 2 <-> 3, 3 <-> 4, 4 <-> 5, 5 <-> 6, 6 <-> 7, 7 <-> 1}]
    ]
]

enter image description here

Let's show that this really finds an isomorphic graph, without need for explicitly using labels from the big graph:

HighlightGraph[bmg, 
  FindSubgraph[
    bmg, 
    Graph[{"ape" <-> "nut", "nut" <-> "mouse", "mouse" <-> "dad", 
           "dad" <-> "sheep", "sheep" <-> "goat", "goat" <-> "ape"}
    ]
  ]
]

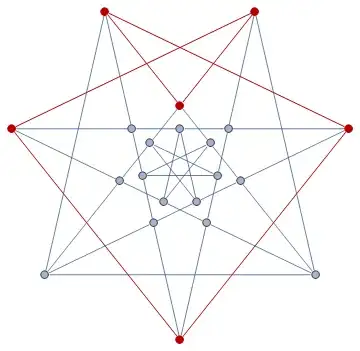
enter image description here

With this function in place, it is easy to find the SubgraphIsomorphismQ function:

SubgraphIsomorphismQ[big_?UndirectedGraphQ, small_?UndirectedGraphQ] :=
   Length[EdgeList@FindSubgraph[big, small]] == Length[EdgeList@small]

Test

SubgraphIsomorphismQ[bmg, Graph[{1 <-> 2, 2 <-> 3, 3 <-> 1}]]

False

(indeed, there is no loop with three nodes)

SubgraphIsomorphismQ[bmg, Graph[{1 <-> 2, 2 <-> 3, 3 <-> 4}]]

True

Szabolcs' example from the comments:

SubgraphIsomorphismQ[Graph[{1 <-> 2, 2 <-> 3, 1 <-> 3, 3 <-> 4}], Graph[{1 <-> 2, 1 <-> 4}]]

True

Older stuff: labeled graphs only

SubgraphQ[bigGraph_, smallGraph_] := 
 With[{undirRule = UndirectedEdge[a__] :> UndirectedEdge @@ Sort[{a}]},
   Intersection[EdgeList[bigGraph] /. undirRule, EdgeList[smallGraph] /. undirRule] 
           ===  Sort[EdgeList[smallGraph] /. undirRule]
  ]

g = CompleteGraph[5];
h = Subgraph[g, {1, 2, 3}]

SubgraphQ[g, h]

True

SubgraphQ[h, g]

False

@PinoAir It sorts the vertices in undirected edges in canonical order so that there is no difference between 1 <->2 and 2<->1. If you don't do this you might not recognize two vertices as the same just because their nodes are ordered differently. I don't do this for directed edges as I assume that order matters there. — Sjoerd C. de Vries, Apr 13 '13 at 21:56
I believe you should be able to write: undirRule = a_UndirectedEdge :> Sort[a] -- Sort works on heads besides List. (Sorry for the non-vote but I cannot test this as you know.) — Mr.Wizard, Apr 13 '13 at 22:45
@Sjoerd Unfortunately this is incorrect, unless you consider the graphs to be labelled (but in that case isomorphism is not an issue). Consider: big = Graph[{1 <-> 2, 2 <-> 3, 1 <-> 3, 3 <-> 4}], small = Graph[{1 <-> 2, 1 <-> 4}]. small is clearly a subgraph of big in the usual unlabelled sense, but the function says it isn't. — Szabolcs, Apr 13 '13 at 23:30
@PinoAir You should clarify if you mean the labelled or unlabelled case. When talking about isomorphism, people usually mean the unlabelled case as the labelled one is trivial. — Szabolcs, Apr 13 '13 at 23:31
@PinoAir You could consider extending Mark McClure's IGraphLink with this functionality and sending a pull request. — Szabolcs, Apr 13 '13 at 23:33
@szabolcs I'm far from an expert in graphs. In fact I wasn't even aware of the existence of unlabeled graphs. So, my solution is indeed for labeled graphs only. Does Mathematica actually have unlabeled graphs? Let me look... — Sjoerd C. de Vries, Apr 14 '13 at 07:48
@Sjoerd It's not really a kind of graph, it's more of a description meaning that the vertices are considered indistinguishable. When describing a graph on a computer, it's necessary to assign labels to the vertices, e.g. {1,2,3} and the graph would look like 1 -- 2 -- 3. Saying that two graphs are isomorphic means that the vertices of one can be relabelled so that it will look the same as the other one. 1 -- 2 -- 3 is isomorphic to 1 -- 3 -- 2 because the relabelling {2 -> 3, 3 -> 2} makes their computer-repreesntation the same too. — Szabolcs, Apr 14 '13 at 13:44
@Szabolcs Yeah, I have been doing some Googling in the meantime and found out about unlabeled graphs. I tried to come up with something new to meet these new requirements. Please see update. — Sjoerd C. de Vries, Apr 14 '13 at 19:28
@Sjoerd I'll need some time to take a look. Isomorphism testing is by no means a trivial things and if this does indeed work correctly that means that you've implemented a complete isomorphism tester ... — Szabolcs, Apr 14 '13 at 19:32
@Szabolcs Well, since it is using plenty of ___s, this won't be fast for large graphs. This is really brute-forcing it. I gather there must be more efficient ways to do this. — Sjoerd C. de Vries, Apr 14 '13 at 19:43
@SjoerdC.deVries If this does indeed work, it would be extremely impressive. — PinoAir, Apr 14 '13 at 20:23
@PinoAir There's a big problem in determining a unique sorting of the edges. If that's solved, the problem will be solved. — Sjoerd C. de Vries, Apr 14 '13 at 20:42
@Szabolcs I brute-brute-forced a newer version. Not efficient, but hopefully correct this time. — Sjoerd C. de Vries, Apr 14 '13 at 23:47
@Szabolcs Can you find a counterexample? What I've tried seems to work thus far. — PinoAir, Apr 15 '13 at 11:00

Szabolcs · Answer 2 · 2019-04-23T11:23:34.803

2015 Update:

IGraph/M has three different functions for this: IGSubisomoprhicQ (generic), IGVF2SubisomorphicQ and IGLADSubisomorphicQ. The last one can also check for induced subgraphs (i.e. you can only remove vertices, but not edges).

Demo:

IGLADSubisomorphicQ[CycleGraph[5], GraphData[{"Fullerene", {26, 1}}]]
(* True *)

IGLADSubisomorphicQ[CycleGraph[5], 
 GraphData[{"Fullerene", {26, 1}}], "Induced" -> True]
(* True *)

IGLADGetSubisomorphism[CycleGraph[5], GraphData[{"Fullerene", {26, 1}}]]
(* {<|1 -> 1, 2 -> 7, 3 -> 18, 4 -> 12, 5 -> 6|>} *)

To get a specific mapping, use IGGetSubisomorphism. To get multiple or all mappings, use IGVF2FindIsomorphisms or IGLADFindSubisomorphisms.

Older version

A solution based on IGraphR:

In[23]:= IGraph["graph.subisomorphic.vf2"][GraphData[{"Fullerene", {26, 1}}], CycleGraph[5]]

Out[23]= RObject[{{True}, 
  {1., 2., 0., 0., 0., 0., 5., 3., 0., 0., 0.,
    0., 4., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.}, 
  {1., 2., 8., 13., 7.}}, 
 RAttributes["names" :> {"iso", "map12", "map21"}]]

Note that you also get back one possible mapping.

Oldest version

You can use RLink in Mathematica 9 to access this functionality in the igraph library.

First, start R separately from Mathematica and run install.packages("igraph").

Then start Mathematica and connect to the external R version. On OS X I did this:

<< RLink`
SetEnvironment["DYLD_LIBRARY_PATH" -> "/Library/Frameworks/R.framework/Resources/lib"]
InstallR["RHomeLocation" -> "/Library/Frameworks/R.framework/Resources"]

Load igraph:

REvaluate["library(igraph)"]

Make the function convenient to call from Mathematica (this is for undirected ones only, but you can easily fix it up to work for both):

Clear[subisomophicQ]
subisomophicQ[g1_?GraphQ, g2_?GraphQ] := 
 Extract[RFunction["function (e1,e2) {
        g1 <- graph.edgelist(e1, directed=F);
        g2 <- graph.edgelist(e2, directed=F);
        graph.subisomorphic.vf2(g1,g2,NULL,NULL,NULL,NULL)  
    }"][List @@@ EdgeList[g1], List @@@ EdgeList[g2]], {1, 1, 1}]

Try it:

subisomorphicQ[GraphData[{"Fullerene", {26, 1}}], CycleGraph[5]]

(* ==> True *)

If you remove the Extract part, you'll also get the precise mapping between the bigger and smaller graphs.

Is there something akin to "SubgraphIsomorphismQ" in Mathematica 9?

2 Answers2

Linked