How to fit 3 data sets to a model of 3 differential equations?

Question

I want to fit 3 data sets to a model consisting of 3 differential equations and 7 parameters. I want to find the parameters best fitting to my model.

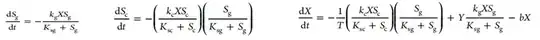
I have searched for several related examples. I borrowed this：https://mathematica.stackexchange.com/questions/28461/how-to-fit-3-data-sets-to-a-model-of-4-differential-equations

sol = ParametricNDSolveValue[{Sg'[t] == -((kg Sg [t] X[t])/(
      Ksg + Sg[t])), Sg[0] == 490, 
    Sc'[t] == -((kc Sc [t] Sg[t] X[t])/((Ksc + Sc[t]) (Ksg + Sg[t]))),
     Sc[0] == 230, 
    X'[t] == -b X[t] - (
      kc Sc[t] Sg[t] X[t])/((Ksc + Sc[t]) (Ksg + Sg[t]) T) + (
      kg Sg[t] X[t] Y)/(Ksg + Sg[t]), X[0] == 22}, {Sg, Sc, X}, {t, 0,
     100}, {kg, Ksg, kc, Ksc, b, T, Y}];
abscissae = {0., 18., 30., 45., 58., 64., 68., 73., 78., 83.5, 90.5, 
   95., 99.};
ordinates = {{490.18, 467.06, 442.16, 420.82, 322.32, 248.67, 209.15, 
    161.54, 98.73, 28.71, 5.34, 0.76, 0.31
    }, {231.3, 232.8, 209.1, 167.1, 127.3, 100.0, 87.5, 76.8, 52.8, 
    52.7, 57.7, 57.0, 58.5}, {22, 30, 36, 60, 77, 92, 107, 115, 125, 
    138, 151, 156, 156}};
data = ordinates;
ListLinePlot[data, DataRange -> {0, 100}, PlotRange -> All, 
 AxesOrigin -> {0, 0}]
transformedData = {ConstantArray[Range@Length[ordinates], 
      Length[abscissae]] // Transpose, 
    ConstantArray[abscissae, Length[ordinates]], data}~
   Flatten~{{2, 3}, {1}};
model[kg_, Ksg_, kc_, Ksc_, b_, T_, Y_][i_, t_] := 
  Through[sol[kg, Ksg, kc, Ksc, b, T, Y][t], List][[i]] /; 
   And @@ NumericQ /@ {kg, Ksg, kc, Ksc, b, T, Y, i, t};
fit = NonlinearModelFit[transformedData, 
   model[kg, Ksg, kc, Ksc, b, T, Y][i, t], {kg, Ksg, kc, Ksc, b, T, 
    Y}, {i, t}, Method -> "Gradient"];
Show[Plot[Evaluate[Table[fit[i, t], {i, 3}]], {t, 0, 100}, 
  PlotLegends -> {Sg, Sc, X}], 
 ListPlot[data, DataRange -> {0, 100}, PlotRange -> All, 
  AxesOrigin -> {0, 0}]]

But it's not working well This is the first time I use MMA for fitting. I would really appreciate your help!