Find all solutions for these two equations

Question

    Clear[x, y]
    eq1 = ((9/10)^x)*Cos[5 x] == y^3
    eq2 =  x^2 + 1 x*y^2 + 3*y^4 - 8*y == 4
    sols = Solve[{eq1, eq2}, {x, y}, Reals]
    ss = Flatten[sol /. C[1] -> 2]
    ss[[2, 2]]

I need to find all solutions for these two equations, is what I am doing correct? Also, how can I plot these two equations on one graph so we can see the intersection?

Do ss = sols // Simplify // N and ContourPlot[Evaluate[{eq1, eq2}], {x, -5, 5}, {y, -3, 3}, Epilog -> {Red, Point[{x, y}] /. ss}] — Akku14, Oct 18 '20 at 13:42
Hi so is this what i do for the first part ss=Simplify[sols[N[1]]] is this correct? — Aran, Oct 18 '20 at 18:26
My ss = sols // Simplify // N is the same as ss = N[Simplify[sols]] . Look into the help manual. If you want only do it for the first solution, do ss1 = N[Simplify[sols[[1]]]] . — Akku14, Oct 18 '20 at 18:31

cvgmt · Accepted Answer · 2020-10-18T14:33:11.363

To Plot the intersection points of the two contours we can also use the tricks of MeshFunction and Mesh

BTW, I also belive that we can extract the intersection points from the ContourPlot, but I'm unable to find the best way.

Clear["`*"]
fun1 = ((9/10)^x)*Cos[5 x] - y^3;
fun2 = x^2 + 1 x*y^2 + 3*y^4 - 8*y - 4;
a = ContourPlot[fun1 == 0, {x, -5, 5}, {y, -5, 5}, 
   MeshFunctions -> {Function[{x, y}, fun1], Function[{x, y}, fun2]}, 
   Mesh -> {{0}}, MeshStyle -> Directive[PointSize[Large], Red], 
   ContourStyle -> Purple];
b = ContourPlot[fun2 == 0, {x, -5, 5}, {y, -5, 5}, 
   ContourStyle -> Cyan];
Show[b, a]

Ulrich Neumann · Answer 2 · 2020-10-19T06:01:13.887

6

Try GraphicsMeshFindIntersections

bild = ContourPlot[{fun1 == 0, fun2 == 0}, {x, -5, 5}, {y, -5, 5}];

intersection points of the two curves in bild

s=   Graphics`Mesh`FindIntersections[bild[[All, 1]] 
(*{{-2.81431, 0.437137}, {-2.19896,0.101216}, {-1.57194, -0.197878},
{-0.931073,-0.395926},{-0.333723, -0.464556}, {0.333229, -0.449604}, 
{0.93169, -0.365035},{1.57238, -0.1831}, {1.72927, -0.122129}, 
{2.19959,0.109049}, {2.74194, 0.674778}}*)
Show[{bild, Graphics[Point[sp]]}]

Sorry, don't know why there is an additional wrong intersection point

edited Oct 19 '20 at 06:01

answered Oct 18 '20 at 14:55

Ulrich Neumann

53,729
2
23
55

Wonderfull! Just what I want to looking for. – cvgmt Oct 18 '20 at 15:02

chris · Answer 3 · 2020-10-18T14:48:58.353

You can use this function FindAllCrossings2D as follows

pts = FindAllCrossings2D[{fux[x, y], fuy[x, y]}, {x, -4, 4}, {y, -4, 
     4}, Method -> {"Newton", "StepControl" -> "LineSearch"}, 
    PlotPoints -> 256, WorkingPrecision -> 20] // Chop

Then

Show[ContourPlot[{fux[x, y] == 0, fuy[x, y] == 0}, 
  {x, -4, 4}, {y, -4,4}],ListPlot[pts]]

Note that the above link provides solutions based on MeshFunction and ListPlot3D

score 3 · Answer 4 · answered Oct 18 '20 at 23:52

Clear["Global`*"]

fun1 = ((9/10)^x)*Cos[5 x] - y^3;
fun2 = x^2 + 1 x*y^2 + 3*y^4 - 8*y - 4;

You can use NSolve with constraints on the variables

sol = NSolve[{fun1 == 0, fun2 == 0, -4 < x < 4, -2 < y < 2}, {x, y}, Reals]
(* {{x -> -2.81502, y -> 0.437016}, {x -> -2.19928, 
  y -> 0.101797}, {x -> -1.57212, y -> -0.198197}, {x -> -0.930805, 
  y -> -0.400714}, {x -> -0.335043, y -> -0.476184}, {x -> 0.334402, 
  y -> -0.460326}, {x -> 0.931406, y -> -0.368789}, {x -> 1.57226, 
  y -> -0.183921}, {x -> 2.19943, y -> 0.107942}, {x -> 2.74341, 
  y -> 0.673483}} *)
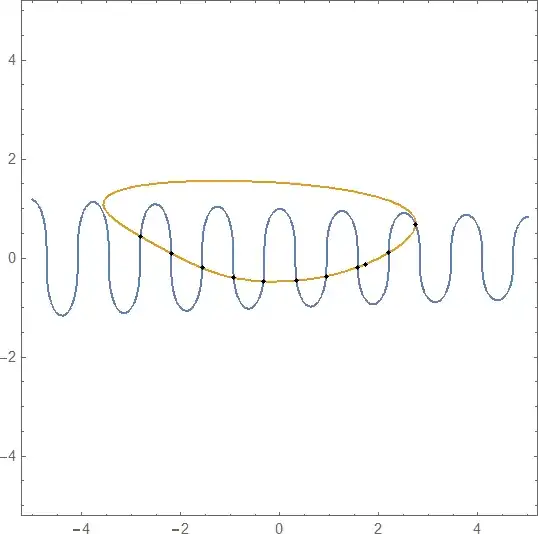
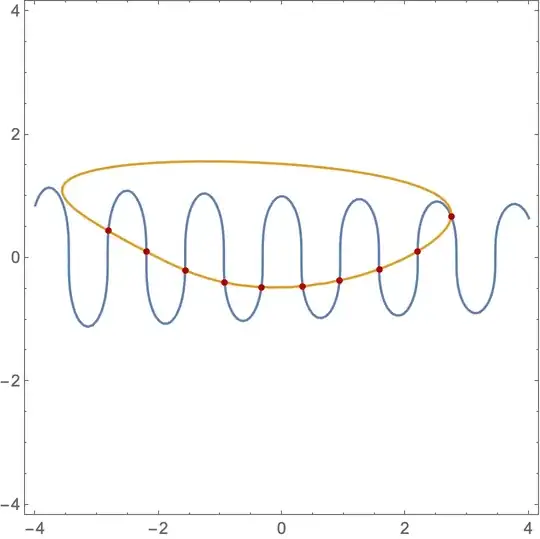
ContourPlot[{fun1, fun2}, {x, -4, 4}, {y, -2, 2},
 FrameLabel -> (Style[#, 14, Bold] & /@ {x, y}), 
 Epilog -> {Red, AbsolutePointSize[4],
   Tooltip[Point[#], #] & /@ ({x, y} /. sol)},
 PlotLegends -> Placed["Expressions", {0.5, 0.125}]]

Find all solutions for these two equations

4 Answers4