I want to solve for X in the equation ode1 (Meaning to leave it alone, or that all the values are on the other side of the equal sign) but the answer it gives me includes to then graph it X vs L but the values on L are changing constantly. Please help
ode1 = (.003) (2.28*-6) + ((1651 - X)*
Sin[3 Degree]) + (((2*(2.27766*-6)*Sqrt[.003])/
Tan[6 Degree])) (Sqrt[.003 + L*Tan[6 Degree]] -
Sqrt[.003]) (1651 - X) - 0.9*(5.67*-8)*(.003*3 Degree*L)*X^4 == 0
sol = Solve[ode1, X, {L, 0, 10}]
Plot[sol, {L, 0, 10}]```

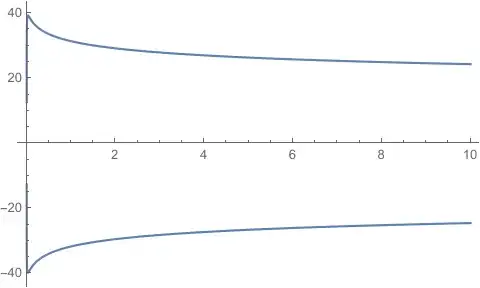
exprs = X /. sol– Michael E2 Oct 24 '20 at 20:51