Can Manipulate controls be generated programmatically based on a (non-manipulated) variable?

Question

I would like to do something like this:

    nSines = 3;
    Manipulate[
            fn = {f1, f2, f3};
            Plot[Evaluate@Table[Sin[fn[[ii]] x], {ii, 1, Length[fn]}], {x, -2 \[Pi], 2 \[Pi]}],
            {{f1, 1}, 1, 6},
            {{f2, 2}, 1, 6},
            {{f3, 3}, 1, 6}
              ]

which generates the following output plot:

But I don't want to hard-code the number of Manipulate controls. So, I'd like to use just the variable nSines in the above example; it's currently unused.

Is there a way to do that? I haven't had any luck putting Table or Sequence as control arguments to Manipulate, but it's definitely possible I just missed the right syntax.

Thanks in advance!!

Answer 1

Yes! The answer is to use a combination of Module, With, and Apply's (@@) to build things. Here's an example:

test[n_] := 
 Module[{x}, 
  With[{vars = Table[x[i], {i, 1, n}]}, 
   Manipulate[ListPlot[vars, PlotRange -> {0, 1}], ##] & @@ 
   MapThread[{#1, #2[[1]], #2[[2]]} &, {vars, Table[{0, 1}, {i, 1, n}]}]]]

This should give a plot of n points which may be manipulated between 0 and 1.

MapThread[{#1, #2[[1]], #2[[2]]} &, {vars, Table[{0, 1}, {i, 1, n}]}] is what builds the "second part" of manipulate; 0 and 1 in Table[{0, 1}, {i, 1, n}] could be replaced with whatever algorithmically-computed ranges you wanted.

Using ## in manipulate to represent a sequence of arguments, and stripping the List head off of the output of MapThread via @@, we get our usual Manipulate configuration.

The substitution of vars with the list of actual variables happens before evaluation via With. Each x[i] functions as a separate variable name here.

The problem now is that all the manipulate sliders have horrible Module names, like x$34213[2], but this can be changed by altering MapThread appropriately!

So, in your case you'll want something like

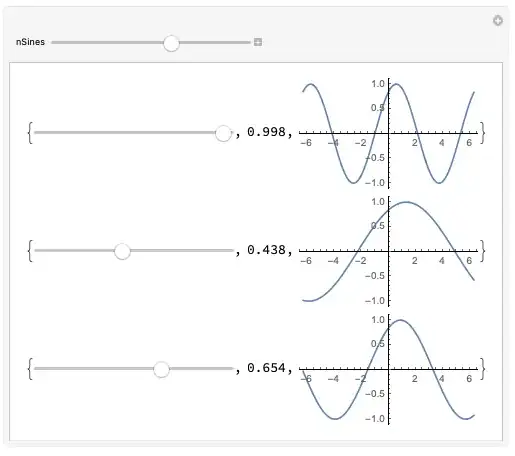
Sines[n_] := 
 Module[{x},
  With[{vars = Table[x[i], {i, 1, n}]},
   Manipulate[
      Plot[
       Evaluate@Table[Sin[vars[[ii]] z], {ii, 1, n}],
       {z, -2 \[Pi], 2 \[Pi]}],
      ##] & @@ 
   MapThread[{{#1, #2, #3}, #4[[1]], #4[[2]]} &,
     {vars, 
      Table[i, {i, 1, n}], (*defaults*)
      Table["f" <> ToString[i], {i, 1, n}], (*slider names*)
      Table[{1, 6}, {i, 1, n}] (*ranges*)}]
  ]]

Note that, for instance, you can also introduce the range for your sliders as a function argument, e.g. define Sines[n_, frange:{_,_}:{1,6}] by changing the defaults to, for example, Table[frange[[1]] + i (frange[[2]] - frange[[1]])/n, {i, 0, n - 1}], and the ranges to Table[frange, {i, 1, n}]. (Sines[4] will still produce four sine waves with {1,6} as the default range under this definition.)

(Also, I'd recommend changing the default provided in the original one way or another, as for n>6, the sliders will start out-of-bounds.)

(Note also that we can also make things a bit more compact by using Evaluate[Sin[# z] & /@ vars] in Plot instead!)

Let me know if you're unfamiliar with any of the parts of Mathematica I've used and want to know how they work!

For fun, here's way too many.

Answer 2

Not exactly what you want (as of yet, I'll come back to this), but it has a simplicity on which you might easily build:

Manipulate[
 Column[
  DynamicModule[{d},
     {Slider[Dynamic[d]],
      Dynamic[d],
      Dynamic[Plot[Sin[1 + d x], {x, -2 \[Pi], 2 \[Pi]}]]
      }] & /@ Range[nSines]
  ],
 {{nSines, 1}, 1, 5}
 ]

Which can give you output like the following when nSines = 3