I'm very new to Mathematica.
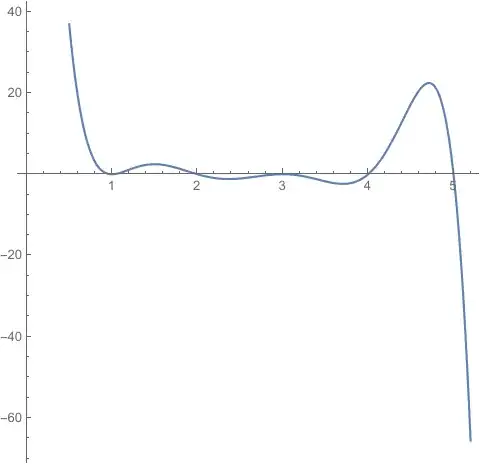
The only roots of a polynomial are 1, 2, 3, 4, and 5. The polynomial is positive on (-∞, 1), (1, 2), (4, 5) and negative on (2, 3), (3, 4), and (5, ∞). Give a polynomial of the smallest degree that satisfies these conditions. Make the leading coefficient 1 or -1.