Exporting several Pyramid to a stl file

Question

I made some 3D structure including several Pyramid and tried to export it to stl file.

(I have referenced this link : Exporting several prisms (or Polyhedrons) to stl (with filled inner space))

It consists of 16 pyramids (4 pyramids for one side)

pyramid16 = {Pyramid[{{Sqrt[3]/2, 1/2, 19 Sqrt[3]}, {0, 1, 
      19 Sqrt[3]}, {0, -1, 19 Sqrt[3]}, {Sqrt[3]/2, -(1/2), 
      19 Sqrt[3]}, {0, 0, Sqrt[3/2]/2 + 19 Sqrt[3]}}], 
   Pyramid[{{0, 1, 19 Sqrt[3]}, {-(Sqrt[3]/2), 1/2, 
      19 Sqrt[3]}, {-(Sqrt[3]/2), -(1/2), 19 Sqrt[3]}, {0, -1, 
      19 Sqrt[3]}, {0, 0, Sqrt[3/2]/2 + 19 Sqrt[3]}}], 
   Pyramid[{{Sqrt[3]/2, 1/2, 19 Sqrt[3]}, {0, 1, 19 Sqrt[3]}, {0, -1, 
      19 Sqrt[3]}, {Sqrt[3]/2, -(1/2), 19 Sqrt[3]}, {0, 
      0, -(Sqrt[(3/2)]/2) + 19 Sqrt[3]}}], 
   Pyramid[{{0, 1, 19 Sqrt[3]}, {-(Sqrt[3]/2), 1/2, 
      19 Sqrt[3]}, {-(Sqrt[3]/2), -(1/2), 19 Sqrt[3]}, {0, -1, 
      19 Sqrt[3]}, {0, 0, -(Sqrt[(3/2)]/2) + 19 Sqrt[3]}}], 
   Pyramid[{{Sqrt[3]/2, 1/2, 18 Sqrt[3]}, {0, 1, 18 Sqrt[3]}, {Sqrt[
      3]/2, 1/2, 19 Sqrt[3]}, {(3 Sqrt[3])/4, 1/4, (37 Sqrt[3])/
      2}, {-((37 Sqrt[3])/4) + 
       1/2 (Sqrt[3/2]/2 + 19 Sqrt[3]), -(111/4) + 
       1/2 Sqrt[3] (Sqrt[3/2]/2 + 19 Sqrt[3]), (37 Sqrt[3])/2}}], 
   Pyramid[{{0, 1, 18 Sqrt[3]}, {-(Sqrt[3]/4), 5/4, (37 Sqrt[3])/
      2}, {0, 1, 19 Sqrt[3]}, {Sqrt[3]/2, 1/2, 
      19 Sqrt[3]}, {-((37 Sqrt[3])/4) + 
       1/2 (Sqrt[3/2]/2 + 19 Sqrt[3]), -(111/4) + 
       1/2 Sqrt[3] (Sqrt[3/2]/2 + 19 Sqrt[3]), (37 Sqrt[3])/2}}], 
   Pyramid[{{Sqrt[3]/2, 1/2, 18 Sqrt[3]}, {0, 1, 18 Sqrt[3]}, {Sqrt[
      3]/2, 1/2, 19 Sqrt[3]}, {(3 Sqrt[3])/4, 1/4, (37 Sqrt[3])/
      2}, {-((37 Sqrt[3])/4) + 
       1/2 (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), -(111/4) + 
       1/2 Sqrt[3] (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), (37 Sqrt[3])/2}}],
    Pyramid[{{0, 1, 18 Sqrt[3]}, {-(Sqrt[3]/4), 5/4, (37 Sqrt[3])/
      2}, {0, 1, 19 Sqrt[3]}, {Sqrt[3]/2, 1/2, 
      19 Sqrt[3]}, {-((37 Sqrt[3])/4) + 
       1/2 (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), -(111/4) + 
       1/2 Sqrt[3] (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), (37 Sqrt[3])/2}}],
    Pyramid[{{-(Sqrt[3]/2), 1/2, 19 Sqrt[3]}, {-(Sqrt[3]/2), 1, (
      37 Sqrt[3])/2}, {-(Sqrt[3]/2), -1, (37 Sqrt[3])/
      2}, {-(Sqrt[3]/2), -(1/2), 
      19 Sqrt[3]}, {-(Sqrt[(3/2)]/2) - Sqrt[3]/2, 0, (37 Sqrt[3])/
      2}}], Pyramid[{{-(Sqrt[3]/2), 1, (37 Sqrt[3])/2}, {-(Sqrt[3]/2),
       1/2, 18 Sqrt[3]}, {-(Sqrt[3]/2), -(1/2), 
      18 Sqrt[3]}, {-(Sqrt[3]/2), -1, (37 Sqrt[3])/
      2}, {-(Sqrt[(3/2)]/2) - Sqrt[3]/2, 0, (37 Sqrt[3])/2}}], 
   Pyramid[{{-(Sqrt[3]/2), 1/2, 19 Sqrt[3]}, {-(Sqrt[3]/2), 1, (
      37 Sqrt[3])/2}, {-(Sqrt[3]/2), -1, (37 Sqrt[3])/
      2}, {-(Sqrt[3]/2), -(1/2), 
      19 Sqrt[3]}, {Sqrt[3/2]/2 - Sqrt[3]/2, 0, (37 Sqrt[3])/2}}], 
   Pyramid[{{-(Sqrt[3]/2), 1, (37 Sqrt[3])/2}, {-(Sqrt[3]/2), 1/2, 
      18 Sqrt[3]}, {-(Sqrt[3]/2), -(1/2), 
      18 Sqrt[3]}, {-(Sqrt[3]/2), -1, (37 Sqrt[3])/
      2}, {Sqrt[3/2]/2 - Sqrt[3]/2, 0, (37 Sqrt[3])/2}}], 
   Pyramid[{{(3 Sqrt[3])/4, -(1/4), (37 Sqrt[3])/2}, {Sqrt[3]/
      2, -(1/2), 19 Sqrt[3]}, {0, -1, 18 Sqrt[3]}, {Sqrt[3]/2, -(1/2),
       18 Sqrt[3]}, {-((37 Sqrt[3])/4) + 
       1/2 (Sqrt[3/2]/2 + 19 Sqrt[3]), 
      111/4 - 1/2 Sqrt[3] (Sqrt[3/2]/2 + 19 Sqrt[3]), (37 Sqrt[3])/
      2}}], Pyramid[{{Sqrt[3]/2, -(1/2), 19 Sqrt[3]}, {0, -1, 
      19 Sqrt[3]}, {-(Sqrt[3]/4), -(5/4), (37 Sqrt[3])/2}, {0, -1, 
      18 Sqrt[3]}, {-((37 Sqrt[3])/4) + 
       1/2 (Sqrt[3/2]/2 + 19 Sqrt[3]), 
      111/4 - 1/2 Sqrt[3] (Sqrt[3/2]/2 + 19 Sqrt[3]), (37 Sqrt[3])/
      2}}], Pyramid[{{(3 Sqrt[3])/4, -(1/4), (37 Sqrt[3])/2}, {Sqrt[
      3]/2, -(1/2), 19 Sqrt[3]}, {0, -1, 18 Sqrt[3]}, {Sqrt[3]/
      2, -(1/2), 
      18 Sqrt[3]}, {-((37 Sqrt[3])/4) + 
       1/2 (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), 
      111/4 - 1/2 Sqrt[3] (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), (
      37 Sqrt[3])/2}}], 
   Pyramid[{{Sqrt[3]/2, -(1/2), 19 Sqrt[3]}, {0, -1, 
      19 Sqrt[3]}, {-(Sqrt[3]/4), -(5/4), (37 Sqrt[3])/2}, {0, -1, 
      18 Sqrt[3]}, {-((37 Sqrt[3])/4) + 
       1/2 (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), 
      111/4 - 1/2 Sqrt[3] (-(Sqrt[(3/2)]/2) + 19 Sqrt[3]), (
      37 Sqrt[3])/2}}]};
Needs["NDSolveFEM"]
c = RegionUnion[pyramid16];
d = MeshRegion@
  ToElementMesh[c, MaxCellMeasure -> Infinity, "MeshOrder" -> 1]
Export["why.stl", d]

It looks complicated, but pyramid16 is a just list of 16 pyramids. This one works but in a weird way.

And the next approach didn't work.

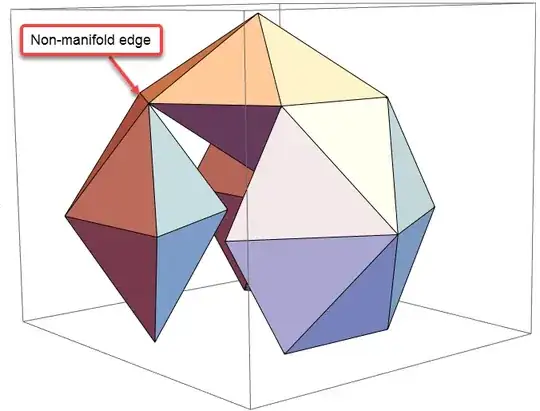
I have confirmed that the first method succeeds for the simple 2~3 pyramids, but when the number of pyramids increase and become complex like this, they are exported strangely. Is there a way to make the stl file neatly as the last picture looks?

Answer 1

Updated answer to include a single STL file

The STL format supports a named solid structure that will allow multiple STL solids to be included in a single file. This will allow us to mesh each disjoint solid separately under a unique name and combine the solids into a single STL file. Note that the STL format is simply a collection of triangles and will not care if there are non-manifold edges in the file.

I defined a helper function called namedSTL to help in the construction of the STL string. I also split each pyramid into two tetrahedra since a tetrahedron is the most primitive solid shape and that may be more robust than using a more complex shape.

(* load required FEM package *)
Needs["NDSolve`FEM`"]
(* function to create a named STL file *)
Clear[namedSTL]
namedSTL[tets_, n_, name_] := Module[{start, finish , mesh, l, stl},
  start = 8 (n - 1) + 1;
  finish = start + 7;
  mesh = ToBoundaryMesh@RegionUnion[tets[[start ;; finish]]];
  SetDirectory[NotebookDirectory[]];
  Export["_stl_temp.stl", 
   Graphics3D[ElementMeshToGraphicsComplex[mesh]], {"STL", 
    "BinaryFormat" -> False}];
  l = StringSplit[ReadString["_stl_temp.stl"], "\r\n"];
  l[[1]] = "solid " <> name;
  l[[-1]] = "endsolid " <> name;
  stl = StringRiffle[l, "\n"];
  stl
  ]
(* split pyramids into two tetrahedra *)
tet32 = Flatten@
   Normal[pyramid16 /. {Pyramid[vtx_] :> 
       GraphicsComplex[
        vtx, {Tetrahedron[{{1, 2, 3, 5}}], 
         Tetrahedron[{{1, 3, 4, 5}}]}]}];

The following workflow will create four named STL shapes for the four disjoint regions and combine them into a single STL file.

(* create a separate named STL file for each disjoint region *)
stlTop = namedSTL[tet32, 1, "Top"];
stlTwo = namedSTL[tet32, 2, "Two"];
stlThree = namedSTL[tet32, 3, "Three"];
stlFour = namedSTL[tet32, 4, "Four"];
(* combine the named STL strings *)
totstl = StringRiffle[{stlTop, stlTwo, stlThree, stlFour}, "\n"];
Export["totstl.stl", totstl, "Text"];
Import["totstl.stl"]

The imported mesh looks as intended. We can use the function FindMeshDefects to find the non-manifold vertices and edges (which Mathematica calls singular edges and singular vertices) that could cause problems with any downstream process.

FindMeshDefects@Import["totstl.stl"]

Original extended comment

Here is an extended comment to the OP question in the comments about "non-manifold edges".

In my quick search, I found a very practical explanation of non-manifold on the TransMagic website. Essentially, manifold means manufacturable (i.e., the final part could be machined from a single block of material) as shown below:

As you can see from your geometry, you have volumetric diamond shaped bodies that are connected to each other through a non-volumetric edge. I highlighted one of these edges as shown below:

This part could not be machined, printed, nor FEM meshed. You would have to add a bevel or fillet to get some sort of finite volume to connect the "disjoint" regions.