6

I have done fitting of data points with a given model that has two parameters (A and B), using NonlinearModelFit. The result of the fit is the maximum of the likelihood function, aka the best fit, and the best values for parameters A and B, say (A0, B0). On the A-B plot this would be a single point. There is also a standard deviation given for both parameters separately σA and σB. However, the likelihood function should also give a region on A-B diagram, therefore possible values for A and B that give a good fit - the one that is under a certain confidence level, like 68%. This region is not exactly {A-σA, A+σA} × {B-σB, B+σB}. Instead, {A-σA, A+σA} is probably projection of this region on A-axis.

How to get the region of A-B dependence with a specified confidence level (.68, .95, .99) coming from the fit?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Vladimir
  • 1,503
  • 1
  • 12
  • 28

1 Answers1

9

The output of the "ParameterConfidenceRegion" can in fact be directly fed into Graphics[], like so:

data = {{0., 1.}, {1., 0.}, {3., 2.}, {5., 4.}, {6., 4.}, {7., 5.}};
nlm = NonlinearModelFit[data, Log[a + b x^2], {a, b}, x];

Graphics[nlm["ParameterConfidenceRegion", ConfidenceLevel -> 0.95], Frame -> True]

confidence ellipse for 95% confidence

You can grab confidence ellipses for multiple confidence levels:

ells = Table[nlm["ParameterConfidenceRegion", ConfidenceLevel -> c], {c, {.68, .95, .99}}];

Graphics[{{Directive[AbsolutePointSize[4], Red],
           Point[{a, b} /. nlm["BestFitParameters"]]},
          Dashed, MapThread[Tooltip[{#1, #2}, StringForm["α = `1`", InputForm[#3]]] &,
                  {ColorData[1] /@ Range[3], ells, {.68, .95, .99}}]}, Frame -> True]

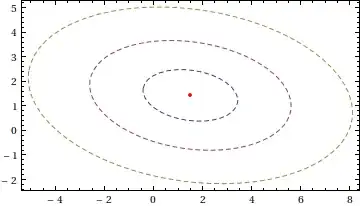
multiple confidence ellipses

(You won't see it in the picture here, but if you execute the last graphic in Mathematica, each confidence ellipse will have an associated tooltip corresponding to its confidence level.)

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
  • This is very nice, thank you! However, I am facing with a new problem now. I have three parameters, but I am interested in only two of them. How to get an ellipse from the ellipsoid? I'm not even sure (mathematically) should one integrate over the third variable or project the ellipsoid on a plane. Either way I am not sure how to calculate it... Do you have some advice? – Vladimir Apr 17 '13 at 03:39
  • @Vlad, I'll need to think about how to slice a 3D ellipsoid; if memory serves, slicing is not too straightforward... anyway, for realism, maybe you can edit your question to include (possibly a simplified version of) your data and three-parameter model. – J. M.'s missing motivation Apr 17 '13 at 03:47
  • Yes, I'm thinking of it, too. But would that be the right thing to do, I mean statistically? – Vladimir Apr 17 '13 at 03:49
  • 3
    @Vladimir You might be interested in this answer – rm -rf Apr 17 '13 at 03:53
  • 1
    The second graphic doesn't work in version 7 (FittedModelsParameterEllipsoid is not a Graphics primitive or directive.`); do you know a way around that? – Mr.Wizard Jul 30 '13 at 22:05