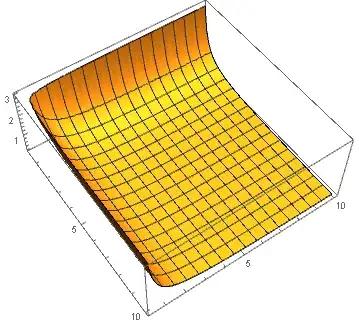
How to create a 3D plot with inclined axes?

Question

I want to create a 3D plot with inclined axes.

For example, I want to change angle between x and y.

plot = Plot3D[{1/x + 1/y}, {x, 0, 10}, {y, 0, 10}, ClippingStyle -> None]

To change angle I can use GeometricTransformation and ShearingMatrix, but it works only for plot without axes and labels.

Graphics3D[{GeometricTransformation[{plot[[1]]}, ShearingMatrix[-Pi/4, {1, 0, 0}, {0, 1, 0}] ]}]

How can I transform axes and add labels?

score 3 · Answer 1 · answered Nov 15 '20 at 08:20

3

In your Graphics3D the Axes are not shown simply because False is the default value for that option. So just add them:

plot = Plot3D[{1/x + 1/y}, {x, 0, 10}, {y, 0, 10}, ClippingStyle -> None];
Graphics3D[GeometricTransformation[plot[[1]], 
  ShearingMatrix[-Pi/4, {1, 0, 0}, {0, 1, 0}]], Axes -> True]

Is that all you needed?

answered Nov 15 '20 at 08:20

M.R.

31,425
8
90
281

No, I want to have the same angle between axes too (add same transform for axes). – Aracturat Nov 15 '20 at 08:29

score 2 · Accepted Answer · edited Nov 15 '20 at 16:24

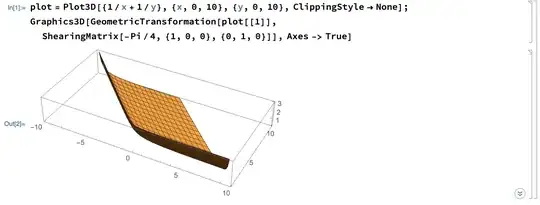
If you did not need the axes and ticks, you could have added a Cuboid with appropriate coordinates before transformation:

Graphics3D[{GeometricTransformation[{plot[[1]], 
      EdgeForm[Red], FaceForm[], Cuboid @@ Transpose @ PlotRange @ plot}, 
   ShearingMatrix[-Pi/4, {1, 0, 0}, {0, 1, 0}]]}]

To add axes and ticks you can use

boxF[5, 5][plot]

Graphics3D[{GeometricTransformation[{plot[[1]], 
    First[ boxF[5, 5][plot]]}, 
   ShearingMatrix[-Pi/4, {1, 0, 0}, {0, 1, 0}]]}, Boxed->False]

using slight modifications of the functions tickF, axesF and boxF from this answer:

ClearAll[tickF, axesF, boxF]
tickF[div1_, div2_: 1, tl_: .03] := Module[{min = #, max = #2}, 
   Select[min <= #[[1]] <= max &]@
    Charting`ScaledTicks[{Identity, Identity}, 
      "TicksLength" -> {tl, tl/2}][min, max, {div1, div2}]] &
axesF[div1_, div2_: - 1, tl_: .03][gr_] := Module[{pr = PlotRange[gr]}, 
   Module[{del = Max[- Subtract @@@ pr], ticks = tickF[div1, div2, tl] @@@ pr, 
     minmax = Transpose[pr], min, max},
   {min, max} = minmax;
    Flatten@{{GrayLevel[0.4], 
     Text[#2, {0, -del/20, 0} + {#1, min[[2]], min[[3]]}], 
     Line[ {min, {max[[1]], min[[2]], min[[3]]}}], 
     Line[ {{#1, min[[2]], min[[3]]}, 
        {#1, min[[2]] + del #3[[1]], min[[3]]}}]} & @@@ ticks[[1]], 
     {Text[#2, {0., 0., del/20} + {min[[1]], #1, max[[3]]}], 
      Line[ {{min[[1]], min[[2]], max[[3]]}, {min[[1]], max[[2]], max[[3]]}}], 
      Line[{{min[[1]], #1, max[[3]]}, 
         {min[[1]], #1, max[[3]] - del #3[[1]]}}]} & @@@ ticks[[2]], 
     {Text[#2, {-del/20, 0., 0} + {min[[1]], min[[2]], #1}], 
      Line[ {min, {min[[1]], min[[2]], max[[3]]}}], 
      Line[ {{min[[1]], min[[2]], #1},
         {min[[1]], min[[2]] + del #3[[1]], #1}}]} & @@@ ticks[[3]]}]];
boxF[div1_, div2_: - 1, tl_: .03][gr_] := 
  Graphics3D[{axesF[div1, div2, tl][gr], gr[[1]], 
    EdgeForm[{AbsoluteThickness[.2], GrayLevel[.4]}], FaceForm[], 
    Cuboid @@ (Transpose[PlotRange[gr]])}, Boxed -> False];

How to create a 3D plot with inclined axes?

2 Answers2