Hyperbola problem

Question

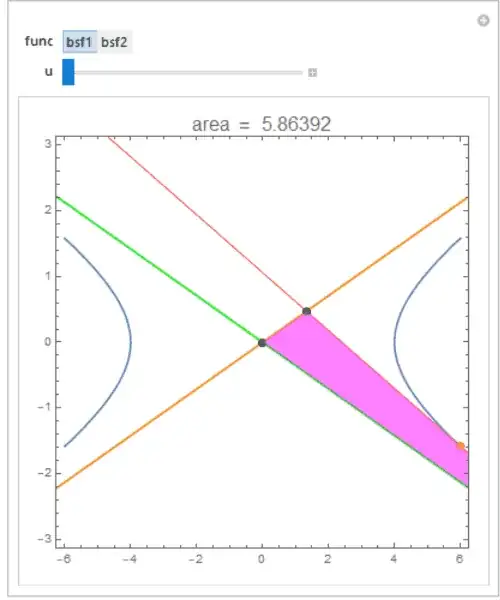
I'm studying the hyperbola given by the implicit function $x^2/16-y^2/2=1$

I need plot the hyperbola and the asymptotes $y=b/a\,x$ and $y=-b/a\,x$. Then I need to select a point on the hyperbola and show the tangent line at that point. Also, I need to show the points of intersection of the tangent with the asymptotes, which will make a triangle with the origin. Finally, I need find the area of the triangle.

Here what I have tried so far:

a = x^2/16 - y^2/2 == 1;
as1 = Sqrt[2] x/4;
as2 = -Sqrt[2] x/4;
Show[
  ContourPlot[x^2/16 - y^2/2 == 1, {x, -5, 5}, {y, -4, 4}], 
  Plot[{as1, as2}, {x, -5, 5}]]

Answer 1

It is well know that the hyperbola equation is $$ \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$ The asymptotes of the hyperbola is $$ \frac{x^2}{a^2}-\frac{y^2}{b^2}=0$$ It's tangent line at point $(x_0,y_0)$ is $$ \frac{x x_0}{a^2}-\frac{y y_0}{b^2}=1$$

sol = Solve[x^2/16 - y^2/2 == 1 &&  x > 0 && y > 0, Reals];
{x0, y0} = {x, y} /. First@sol /. x -> 5;
contours = 
  ContourPlot[{x^2/16 - y^2/2 == 1, x^2/16 - y^2/2 == 0, 
    x*x0/16 - y*y0/2 == 1}, {x, -10, 10}, {y, -10, 10}, 
   Epilog -> {Red, Point[{x0, y0}]}, AspectRatio -> Automatic, 
   ContourStyle -> {Red, Green, Blue}];
reg = ImplicitRegion[{x^2/16 - y^2/2 <= 1, x^2/16 - y^2/2 >=  0, 
   x*x0/16 - y*y0/2 <=  1}, {{x, 0, 10}, {y, -10, 10}}];
regfigure = 
 RegionPlot[reg, PlotPoints -> 80, PlotStyle -> Orange];
reg // Area
Show[contours, regfigure, PlotRange -> All]

4 Sqrt[2]

Answer 2

a = x^2/16 - y^2/2 == 1;
as1 = Sqrt[2] x/4;
as2 = -Sqrt[2] x/4;

cp = ContourPlot[x^2/16 - y^2/2 == 1, {x, -6, 6}, {y, -4, 4}];

asymptotes = Plot[{as1, as2}, {x, -50, 50}, PlotStyle -> {Orange, Green}];

We get two BSplineFunctions from the two pieces of the contour:

{bsf1, bsf2} = Cases[Normal[cp][[1]], Line[x_] :> BSplineFunction[x], All];

InfiniteLine[bsf1[u], bsf1'[u]] gives th tangent line to the parametric curve bsf1 at point u (similarly, for bsf2):

tngnt1[u_] := Graphics[{Red, InfiniteLine[bsf1[u], bsf1'[u]]}];
tngnt2[u_] := Graphics[{Red, InfiniteLine[bsf2[u], bsf2'[u]]}];

We use Graphics`Mesh`FindIntersections to get the intersections of asymptotes and the selected tangent line:

Manipulate[show0 = Show[asymptotes, If[func === bsf1, tngnt1, tngnt2][u], 
   PlotRange -> PlotRange -> {{-50, 50}, {-10, 10}}];
 intersections = Graphics`Mesh`FindIntersections[show0];
 Show[cp, show0, 
  Graphics@{Red, PointSize[Large], Point[func[u]], Black, 
    Point[intersections], Magenta, Opacity[.5], Polygon[intersections]}, 
  PlotLabel -> Style[PromptForm["area", Area[Polygon@intersections]], 16],
  PlotRange -> {{-6, 6}, {-3, 3}}],
 {{func, bsf1}, {bsf1 -> "bsf1", bsf2 -> "bsf2"}}, {u, 0, 1}]