5

I am a newbie using Mathematica. I wrote this code to plot the roots of Littlewood polynomials, based on the structure of other programming languages. But I'm sure Mathematica has tools to do it in a more condensed and efficient way. Could you guide me how to do it?

poly[exp_, var_] :=
  Times @@@ Tuples[var^Range[0, exp]] //   
  Tuples[{1, -1}, Length@#].# &;

aux[num_] := lista[[num]];


pts = List[];


For[i = 1, i < 15, i++, lista = poly[{i}, {x}];
   For[j = 1, j < Length[lista] + 1, j++,
      pts = Join[pts, ({Re[#1], Im[#1]} &) /@ (x /. 
         NSolve[aux[j] == 0, x])];
   ]
];


graphi = ListPlot[puntos,
         PlotRange -> {{-2.2, 2.2}, {-2.2, 2.2}},
         AspectRatio -> Automatic,
         PlotStyle -> {PointSize[0.0000001],
            Opacity[0.05],
            Yellow
         },
         Axes -> False,
         Background -> Black,
         ImageSize -> 1000,
         GridLines -> {{-2, -1, 0, 1, 2}, {-2, -1, 0, 1, 2}}
];


Export["/Animaciones/Littlewood/14.png", graphi];

Use aux[num_]:=lista[[num]]; because ({Re[#1], Im[#1]} &) /@ (x /.NSolve[lista[[j]] == 0, x]) gave me an error, and pts=List[]; to have an empty list. As seen in the first For, this code generates the roots of the Littlewood polynomials with $n = 14$.

Also, is it normal for Mathematica on Linux (Ubuntu 20.04) to use only one thread at a time in its calculations? I think a lot of processing power is wasted.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Marco García
  • 51
  • 3
  • 3
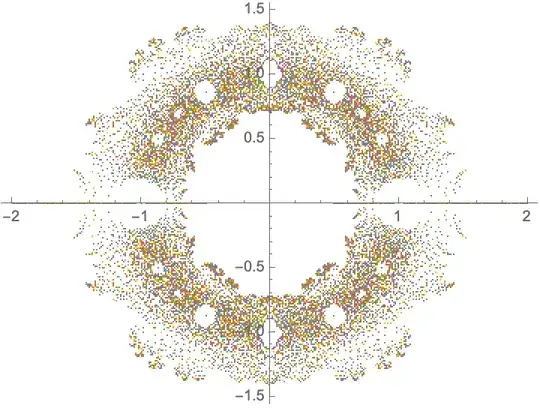
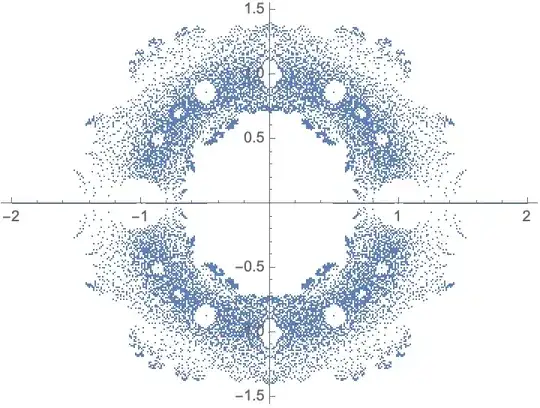
    You can use something like ReIm@Values@NSolve[ lista[[j]] == 0, x] instead as no need for separate Re andIm, and ReIm is listable. You should consider using a Table, or Reap+Sow+Flatten to achieve what's going on in the loops. – flinty Nov 16 '20 at 17:47
  • 1
    Related: https://mathematica.stackexchange.com/q/73312/2090 – chyanog Dec 25 '20 at 04:44

3 Answers3

8

The roots can be represented directly and exactly with Root objects; there is no need to invoke Solve or NSolve explicitly. For a given tuple t we can list them with

F[t_] := Array[Root[#^Range[0, 11].t &, #] &, 11]

or, more generally for arbitrary polynomial degree,

F[t_] := With[{n = Length[t] - 1},
  Array[Root[#^Range[0, n].t &, #] &, n]]

Example:

F[{1, 1, -1}]
(*    {1/2 (1 - Sqrt[5]), 1/2 (1 + Sqrt[5])}    *)

F[{-1, 1, 1, -1, -1, -1, 1, -1, -1, 1, -1, -1}]
(*    {-1.52929, -1.13608, -1., -0.461159 - 0.792192 I, -0.461159 + 0.792192 I,
       0.300042 - 1.08437 I, 0.300042 + 1.08437 I, 0.646434 - 0.281355 I,
       0.646434 + 0.281355 I, 0.847365 - 0.608848 I, 0.847365 + 0.608848 I}    *)

Plot them with ComplexListPlot:

ComplexListPlot[F /@ Tuples[{-1, 1}, 12]]

enter image description here

Alternatively (faster), by taking the product of all of these polynomials and setting this product to zero, we can find all solutions in one go:

With[{n = 11},
  ComplexListPlot[x /. Solve[Times @@ (1 + Tuples[{-1, 1}, n].x^Range[n]) == 0, x]]]

enter image description here

Roman
  • 47,322
  • 2
  • 55
  • 121
7

I thought I'd seen this before!

In-fact you can do all of this and plot it in under 128 characters:

Graphics[{PointSize[Tiny],Point@Flatten[((ReIm[z]/.#)&/@NSolve[z^Range[0,11].#==0,z])&/@Tuples[{-1,1},12],1]}]

enter image description here

The credit goes to Yuncong Ma's Honorable Mention Entry from the 2012 one-liner competition. The terse syntax is explained in the video above, but happy to help break it down further if needed.

With regards to efficiency, I suspect there's improvements to be made - but the bulk of this is spent inside NSolve so perhaps unlikely..

George Varnavides
  • 4,355
  • 12
  • 20
  • 1
    +1 With Manipulate: Manipulate[Graphics[{PointSize[Which[n < 4, Large, n < 6, Medium, n < 9, Small, True, Tiny]], Point@Flatten[((ReIm[z] /. #) & /@ NSolve[z^Range[0, n].# == 0, z]) & /@ Tuples[{-1, 1}, n + 1], 1]}], {{n, 11}, Range[11]}] – Bob Hanlon Nov 16 '20 at 20:50
3

If I use the safened version of DumpsterDoofus's visualization routine with the last formulation in Roman's answer, I get this:

With[{n = 11}, 
     PlotComplexPoints[x /. NSolve[Times @@ (1 + Tuples[{-1, 1}, n].x^Range[n]), x],
                       600, 20, 20, 10, {0.1, 0.3, 1.}]]

Littlewood polynomial roots

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574