I want to plot the following solid nicely.
$\{(\rho\cos\theta\sin\phi,\rho\sin\theta\sin\phi,\rho\cos\phi)\in\mathbb{R}^3\mid(\rho,\phi,\theta)\in[1,2]\times[0,\frac{\pi}{2}]\times[0,\frac{\pi}{2}]\}$.
The following code didn't work:
ParametricPlot3D[{r Cos[t] Sin[s], r Sin[t] Sin[s], r Cos[s]}, {r, 1, 2}, {s, 0, Pi/2}, {t, 0, Pi/2},ImageSize->Large, PlotStyle->Blue]
Please tell me how to do.
ParametricPlot3D[
Table[{r Cos[t] Sin[s], r Sin[t] Sin[s], r Cos[s]}, {r, 1, 2, .02}] //
Evaluate, {s, 0, Pi/2}, {t, 0, Pi/2}, ImageSize -> Large]
Another Way
If we use the implicit expression of sphere, we can also construct the solids and it's complement by a relatively complex way.
SetOptions[ContourPlot3D, Boxed -> False, Axes -> False,
Lighting -> Automatic, BoundaryStyle -> None,
Mesh -> {{0}, {0}, {0}}];
f1 = x^2 + y^2 + z^2 - 1^2;
f2 = x^2 + y^2 + z^2 - 2^2;
f3 = x;
f4 = y;
f5 = z;
pureFun[f_] := (Evaluate[
f /. {x -> Slot@1, y -> Slot@2, z -> Slot@3}]) &;
s1 = ContourPlot3D[f1 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1},
MeshFunctions -> pureFun /@ {f3, f4, f5},
MeshShading -> {{{None, None}, {None, None}}, {{None,
StippleShading[0.9]}, {None, None}}}, MeshStyle -> None];
s2 = ContourPlot3D[f2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f3, f4, f5},
MeshShading -> {{{None, None}, {None, None}}, {{None,
HatchShading[]}, {None, None}}}, MeshStyle -> None];
s3 = ContourPlot3D[f3 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f1, f2, f4, f5},
MeshShading -> {{{{None, None}, {None, None}}, {{None,
None}, {None, None}}}, {{{None,
HalftoneShading[0.6, Orange]}, {None, None}}, {{None,
None}, {None, None}}}}, MeshStyle -> None];
s4 = ContourPlot3D[f4 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f1, f2, f3, f5},
MeshShading -> {{{{None, None}, {None, None}}, {{None,
None}, {None, None}}}, {{{None, None}, {None, None}}, {{None,
HalftoneShading[0.6, Orange]}, {None, None}}}},
MeshStyle -> None];
s5 = ContourPlot3D[f5 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f1, f2, f3, f4},
MeshShading -> {{{{None, None}, {None, None}}, {{None,
HalftoneShading[0.8, Orange]}, {None, None}}}, {{{None,
None}, {None, None}}, {{None, None}, {None, None}}}},
MeshStyle -> None];
Show[s1, s2, s3, s4, s5, PlotRange -> All]
The Complement
SetOptions[ContourPlot3D, Boxed -> False, Axes -> False,
Lighting -> Automatic, BoundaryStyle -> None,
Mesh -> {{0}, {0}, {0}}];
f1 = x^2 + y^2 + z^2 - 1^2;
f2 = x^2 + y^2 + z^2 - 2^2;
f3 = x;
f4 = y;
f5 = z;
pureFun[f_] := (Evaluate[
f /. {x -> Slot@1, y -> Slot@2, z -> Slot@3}]) &;
s1 = ContourPlot3D[f1 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1},
MeshFunctions -> pureFun /@ {f3, f4, f5},
MeshShading -> {{{None, None}, {None, None}}, {{None,
StippleShading[0.9]}, {None, None}}}, MeshStyle -> None];
s2 = ContourPlot3D[f2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f3, f4, f5},
MeshShading -> {{{HatchShading[], HatchShading[]}, {HatchShading[],
HatchShading[]}}, {{HatchShading[], None}, {HatchShading[],
HatchShading[]}}}, MeshStyle -> None];
s3 = ContourPlot3D[f3 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f1, f2, f4, f5},
MeshShading -> {{{{None, None}, {None, None}}, {{None,
None}, {None, None}}}, {{{None,
HalftoneShading[0.6, Orange]}, {None, None}}, {{None,
None}, {None, None}}}}, MeshStyle -> None];
s4 = ContourPlot3D[f4 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f1, f2, f3, f5},
MeshShading -> {{{{None, None}, {None, None}}, {{None,
None}, {None, None}}}, {{{None, None}, {None, None}}, {{None,
HalftoneShading[0.6, Orange]}, {None, None}}}},
MeshStyle -> None];
s5 = ContourPlot3D[f5 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
MeshFunctions -> pureFun /@ {f1, f2, f3, f4},
MeshShading -> {{{{None, None}, {None, None}}, {{None,
HalftoneShading[0.8, Orange]}, {None, None}}}, {{{None,
None}, {None, None}}, {{None, None}, {None, None}}}},
MeshStyle -> None];
Show[s1, s2, s3, s4, s5, PlotRange -> All]
For the solid you can also use
pp1 = ParametricPlot3D[
Table[{r Cos[t] Sin[s], r Sin[t] Sin[s], r Cos[s]}, {r, {1, 2}}], {s, 0,
Pi/2}, {t, 0, Pi/2}, ImageSize -> Large];
pp2 = ParametricPlot3D[
Table[{r Cos[t] Sin[s], r Sin[t] Sin[s], r Cos[s]}, {s, {0, Pi/2}}], {r, 1,
2}, {t, 0, Pi/2}, ImageSize -> Large];
pp3 = ParametricPlot3D[
Table[{r Cos[t] Sin[s], r Sin[t] Sin[s], r Cos[s]}, {t, {0, Pi/2}}], {r, 1,
2}, {s, 0, Pi/2}, ImageSize -> Large];
Show[pp1, pp2, pp3]
You can use SphericalShell with RegionPlot3D:
RegionPlot3D[RegionIntersection[Cuboid[{0, 0, 0}, {2, 2, 2}],
SphericalShell[{0, 0, 0}, {1, 2}]],
Axes -> True, PlotPoints -> 50]
RegionPlot3D[Region@SphericalShell[{0, 0, 0}, {1, 2}],
PlotRange -> {{0, 2}, {0, 2}, {0, 2}}, Axes -> True, PlotPoints -> 50]
same picture
Alternatively, you can use ImplicitRegion:
ir = ImplicitRegion[{1 <= x^2 + y^2 + z^2 <= 4, x >= 0, y >= 0, z >= 0}, {x, y, z}]
RegionPlot3D[ir, PlotStyle -> Red, PlotPoints -> 80, Axes -> True]
From How to generate 3D spherical sector :
sphericalSegment[{r1_,
r2_}, {θ1_, θ2_}, {ϕ1_, ϕ2_}] :=
Module[{plot, pts, surf, bdy},
plot = ParametricPlot3D[{Cos[θ] Sin[ϕ],
Sin[θ] Sin[ϕ],
Cos[ϕ]}, {θ, θ1, θ2}, {ϕ, ϕ1, ϕ2},
Mesh -> None, BoundaryStyle -> Black];
pts = First@Cases[plot, GraphicsComplex[p_, ___] :> p, Infinity];
surf = First@Cases[plot, Polygon[p_] :> p, Infinity];
bdy = First@Cases[plot, Line[p_] :> p, Infinity];
GraphicsComplex[
Join[r1*pts, r2*pts], {EdgeForm[], Polygon[surf],
Polygon[Reverse /@ surf + Length@pts],
Polygon[Join[#, Reverse@# + Length@pts],
VertexNormals ->
Cross[Subtract @@ pts[[#]], pts[[First@#]]]] & /@
Partition[bdy, 2, 1, 1]}, VertexNormals -> Join[-pts, pts]]]
Graphics3D[sphericalSegment[{1, 2}, {0, Pi/2}, {0, Pi/2}]]
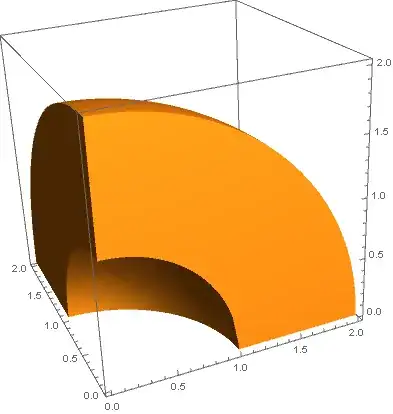
Graphics3D[sphericalSegment[{1, 2}, {0, Pi/2}, {0, Pi/2}]]) -- Related: https://mathematica.stackexchange.com/questions/17464/plotting-a-3d-sphere-i-e-how-to-vizualise-the-spanned-volume-int-02-pi-int/17466#17466 – Michael E2 Nov 17 '20 at 02:12