Use of ParallelDo with an iterative or recursive calculation

Question

Is it possible to use ParallelDo (or any similar parallelization method) to speed up the calculation of an iterative calculation, which takes a previous calculation result as input to new calculation? It seems to me not possible conceptually, since each round will have to wait for the first to get its input, but I wonder if there are ways around this?

For example, if f1[r] is some predefined arbitrary continuous input function and f2[r] is some output function (over the r variable that runs from 0 to some number a, with some step called step, e.g. say step=a/100), then a calculation like this example

f1=1;
Do[
Do[
f2[r2]=NIntegrate[r1 f1[r1] BesselJ[0, r1 r2] E^(-I (r1^2 + r2^2)/2),{r1,0,a}],
(r2,0,a,step)];
f1=Interpolation[Table[{r2,f2[r2]},{r2,0,a,step}]],
{kk,100}]

would be difficult to speed up by parallelization (e.g. using ParallelDo), right?

Are there any suggestions to speed this up by parallel methods or other methods that are not to too difficult for a beginner in Mathematica to understand?

Answer 1

The only thing that can be parallelized here is the generation of the interpolation points. For example:

Clear[integrate, interpolate];
integrate[f_, r2_?NumericQ, a_?NumericQ] := NIntegrate[
   r1 f[r1] BesselJ[0, r1 r2] E^(-I (r1^2 + r2^2)/2),
   {r1, 0, a}
];
interpolate[f_, a_?NumericQ, step_?NumericQ] := Interpolation[
  ParallelTable[
    {r2, integrate[f, r2, a]},
    {r2, 0, a, step}
  ]
];

Iterate the procedure twice, starting with a constant function:

results = NestList[
   interpolate[#, 1, 0.01] &,
   1 &,
   2
];

Plot the obtained functions at each iteration:

ReImPlot[Evaluate[Through[results[r2]]],
  {r2, 0, 1},
  PlotLegends -> Range[0, Length[results] - 1]
]

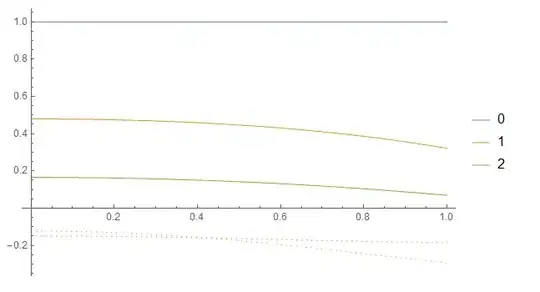
Edit

I don't think that with NIntegrate you can speed this up any further. The free parameter r2 appears in the body of the integral, so I don't think that interpolation is going to help you too much here. You could make an interpolation over both r1 and r2 of which you then take the antiderivative over r1, but you also risk introducing numerical error that way. There's probably a reason why NIntegrate isn't faster here.

I do have another idea for speeding this up, though. We can use ParametricNDSolveValue to do the integration instead by re-phrasing the problem and considering r2 to be a parameter. This should reduce the top-level overhead involved in calling NIntegrate multiple times. Here's how to do it:

Clear[integrate, interpolate];
integrate[f_, a_?NumericQ] := ParametricNDSolveValue[
   {y'[r1] == r1 f[r1] BesselJ[0, r1 r2] E^(-I (r1^2 + r2^2)/2), y[0] == 0},
   y[a],
   {r1, 0, a},
   {{r2, 0, a}}
];
interpolate[f_, a_?NumericQ, step_?NumericQ] := With[{
  int = integrate[f, a]
},
  Interpolation[
    ParallelTable[
      {r2, int[r2]},
      {r2, 0, a, step},
      Method -> "CoarsestGrained"
    ]
  ]
];
results = NestList[interpolate[#, 1, 0.01]&, 1&, 20];
ReImPlot[
  Evaluate[Through[results[r2]]],
  {r2, 0, 1},
  PlotLegends -> Range[0, Length[results] - 1], PlotRange -> All
]

This should be significantly faster than the method based on NIntegrate. You can also take a look at FunctionInterpolation to do the Interpolation step, since this might save you from having to sub-sample the integral more than you really need. For example:

int = Quiet @ FunctionInterpolation[
   integrate[1&, 1][r2],
   {r2, 0, 1}, 
   InterpolationPoints -> 50
]
ReImPlot[int[r2], {r2, 0, 1}]

FunctionInterpolation cannot be parallelized, though, so it's a trade-off