I'm trying to use Mathematica (12.0.0) to model radiation chemical kinetics using a known reaction set, in this case it's water radiolysis.
It solves the set of equations I throw at it without any errors, however the InterpolatingFunction it's throwing out for the result is different from expected. The magnitudes in some cases is a bit off and most notably for a number of the products I've specified they are very irregular, being a bit "squiggly" where they should be smooth curves and straight lines.
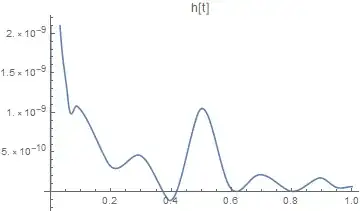
I've put the same reactions/rate constants into other software (FACSIMILE) to show what outputs I should expect. One example below:
H (Mathematica)
H (Facsimile)
As you can see there are 5 peaks over the plot in the Mathematica plot whereas the FACSIMILE plot is smooth. My question is what is causing this behaivour and how can I resolve it?
Code below:
ClearAll["Global'*"]
doserate = 10;
time = 60;
geaqa = 2.61.036410^-7;
gh = 0.61.036410^-7;
goh = 2.71.036410^-7;
gh2 = 0.451.036410^-7;
gh2o2 = 0.71.036410^-7;
kgeaqa = geaqadoserate;
kgh = ghdoserate;
kgoh = gohdoserate;
kgh2 = gh2doserate;
kgh2o2 = gh2o2*doserate;
kw2 = 7.2610^9;
kw3 = 510^9;
kw4 = 4.810^9;
kw5 = 3.410^10;
kw6 = 3.510^10;
kw7 = 1.110^10;
kw8 = 1.410^10;
kw9 = 2.310^10;
kw10 = 1.310^10;
kw11 = 1.310^10;
kw12 = 3.610^7;
kw13 = 1.310^10;
kw14 = 1.1310^10;
kw14a = 1.1410^10;
kw15 = 1.1310^10;
kw16 = 2.910^7;
kw17 = 1.110^10;
kw18 = 8.810^9;
kw19 = 8.410^5;
kw20 = 110^8;
kw21 = 310^-1;
kw22 = 510^5;
kw22a = 2.310^-7;
kw23 = 1.1710^-3;
kw23b = 1.1810^11;
kw24 = 8.910^-2;
kw24b = 4.7810^10;
kw25 = 1.2710^10;
kw25b = 1.410^6;
kw26 = 8.910^-2;
kw26b = 4.7810^10;
kw27 = 1.2710^10;
kw27b = 1.410^6;
kw28 = 4.7810^10;
kw28b = 7.3510^5;
kw29 = 1.2710^10;
kw29b = 1.6310^-1;
kw30 = 5.83;
kw30b = 2.110^10;
kw31 = 2.4410^7;
kw31b = 1.7410^1;
kw32 = 4.5810^-5;
kw32b = 3.9510^7;
rw2 = kw2eaqa[t]^2h2o[t]^2;
rw3 = kw3h[t]^2;
rw4 = kw4oh[t]^2;
rw5 = kw5eaqa[t]h[t]h2o[t];
rw6 = kw6eaqa[t]oh[t];
rw7 = kw7h[t]oh[t];
rw8 = kw8eaqa[t]h2o2[t];
rw9 = kw9eaqa[t]o2[t];
rw10 = kw10eaqa[t]o2a[t]h2o[t];
rw11 = kw11eaqa[t]ho2[t];
rw12 = kw12h[t]h2o2[t];
rw13 = kw13h[t]o2[t];
rw14 = kw14h[t]ho2[t];
rw14a = kw14ah[t]ho2[t];
rw15 = kw15h[t]o2a[t];
rw16 = kw16oh[t]h2o2[t];
rw17 = kw17oh[t]o2a[t];
rw18 = kw18oh[t]ho2[t];
rw19 = kw19ho2[t]^2;
rw20 = kw20o2a[t]ho2[t]h2o[t];
rw21 = kw21o2a[t]^2h2o[t]^2;
rw22 = kw22h2o2[t];
rw22a = kw22ah2o2[t];
rw23 = kw23h2o[t];
rw23b = kw23bhc[t]oha[t];
rw24 = kw24h2o2[t];
rw24b = kw24bho2a[t]hc[t];
rw25 = kw25h2o2[t]oha[t];
rw25b = kw25bho2a[t]h2o[t];
rw26 = kw26oh[t];
rw26b = kw26bhc[t]oa[t];
rw27 = kw27oh[t]oha[t];
rw27b = kw27boa[t]h2o[t];
rw28 = kw28ho2[t];
rw28b = kw28bhc[t]o2a[t];
rw29 = kw29ho2[t]oha[t];
rw29b = kw29bo2a[t]h2o[t];
rw30 = kw30h[t];
rw30b = kw30beaqa[t]hc[t];
rw31 = kw31h[t]oha[t];
rw31b = kw31beaqa[t]h2o[t];
rw32 = kw32h[t]h2o[t];
rw32b = kw32bh2[t]*oh[t];
watersolver = NDSolve[{eaqa'[t] == kgeaqa + rw30 + rw31 - rw2 - rw5 - rw6 - rw8 - rw9 - rw10 - rw11 - rw30b - rw31b,
h2o'[t] == rw7 + rw12 + rw16 + rw18 + rw22 + rw23b + rw25 + rw27 + rw29 + rw31 + rw32b - rw2 - rw5 - rw10 - rw20 - rw21 - rw23 - rw25b - rw27b - rw29b - rw31b - rw32,
h2'[t] == kgh2 + rw2 + rw3 + rw5 + rw32 - rw32b,
oha'[t] == rw2 + rw5 + rw6 + rw8 + rw10 + rw17 + rw20 + rw21 + rw23 + rw25b + rw27b + rw29b + rw31b - rw23b - rw25 - rw27 - rw29 - rw31 ,
oh'[t] == kgoh + rw8 + rw12 + rw14a + rw22a + rw26b + rw27b + rw32 - rw4 - rw6 - rw7 - rw16 - rw17 - rw18 - rw26 - rw27 - rw32b,
h2o2'[t] == kgh2o2 + rw4 + rw10 + rw14 + rw19 + rw20 + rw21 + rw24b + rw25b - rw8 - rw12 - rw16 - rw22 - rw22a - rw24 - rw25,
h'[t] == kgh + rw30b + rw31b + rw32b - rw3 - rw5 - rw7 - rw12 - rw13 - rw14 - rw14a - rw15 - rw30 - rw31 - rw32,
o2a'[t] == rw9 + rw28 + rw29 - rw10 - rw15 - rw17 - rw20 - rw21 - rw28b - rw29b,
ho2a'[t] == rw11 + rw15 + rw24 + rw25 - rw24b - rw25b,
hc'[t] == rw23 + rw24 + rw26 + rw28 + rw30 - rw23b - rw24b - rw26b - rw28b - rw30b,
oa'[t] == rw26 + rw27 - rw26b - rw27b,
o2'[t] == rw17 + rw18 + rw19 + rw20 + rw21 + rw22 - rw9 - rw13,
ho2'[t] == rw13 + rw16 + rw28b + rw29b - rw11 - rw14 - rw14a - rw18 - rw19 - rw20 - rw28 - rw29,
eaqa[0] == 0,
h2o[0] == 55.5,
h2[0] == 0,
oha[0] == 0,
oh[0] == 0,
h2o2[0] == 0,
h[0] == 0,
o2a[0] == 0,
ho2a[0] == 0,
hc[0] == 0,
oa[0] == 0,
o2[0] == 0,
ho2[0] == 0}, {eaqa, h2o, h2, oha, oh, h2o2, h, o2a, ho2a, hc, oa, o2, ho2}, {t, 0, 1}]
I'm fairly new to Mathematica and I'm still trying to learn all its intricacies/limits. Have I missed anything glaring? Is there a better InterpolatingFunction/NDSolve setting for what I'm trying to do? Am I running into some sort of limitation in Mathematica already? Any help on this would be much appreciated.
Many thanks.


MaxStepSize -> 0.001. That seems to make most of the plots smooth, though I don't know enough about the system you're looking at to say if they are correct or not. I did notice that the peak doesn't reach quite as high in Mathematica as it does in your other program. I'm not sure what causes the difference. – MassDefect Nov 19 '20 at 00:00time; however,timesubsequently does not appear anywhere. Should it? – Bob Hanlon Nov 19 '20 at 00:00