Interpolation not working

Question

This is probably a very silly question but I am trying to use Interpolation for the following data:

  data={{0.965251, 0.}, {3.0888, 0.}, {5.98456, 0.}, {9.26641, 0.}, {12.5483,
   0.}, {15.8301, 0.}, {18.1467, 0.}, {21.8147, 0.}, {26.2548, 
  0.}, {30.695, 1.12676}, {33.3977, 1.69014}, {36.8726, 
  2.53521}, {39.3822, 3.38028}, {42.8571, 3.94366}, {45.7529, 
  5.35211}, {48.8417, 6.76056}, {51.5444, 8.73239}, {54.0541, 
  10.9859}, {55.7915, 13.2394}, {58.1081, 16.9014}, {59.0734, 
  19.1549}, {61.0039, 22.8169}, {62.1622, 26.4789}, {63.3205, 
  30.4225}, {64.2857, 34.3662}, {65.0579, 38.3099}, {65.8301, 
  42.8169}, {66.7954, 47.8873}, {67.3745, 53.8028}, {68.3398, 
  60.5634}, {68.9189, 65.6338}, {69.112, 71.5493}, {69.6911, 
  78.0282}, {70.2703, 84.507}, {70.6564, 88.4507}, {70.6564, 
  92.3944}, {71.4286, 97.1831}, {72.5869, 100.563}, {73.7452, 
  98.3099}, {74.5174, 92.6761}, {74.7104, 87.3239}, {75.0965, 
  82.2535}, {75.2896, 77.4648}, {75.6757, 72.1127}, {76.0618, 
  63.3803}, {76.6409, 54.6479}, {77.027, 47.3239}, {77.4131, 
  40.}, {78.3784, 35.2113}, {78.5714, 29.8592}, {80.1158, 
  24.2254}, {81.4672, 22.2535}, {82.8185, 19.7183}, {84.3629, 
  18.8732}, {87.2587, 18.5915}, {91.6988, 18.8732}, {94.5946, 
  18.5915}, {98.2626, 18.3099}, {100., 18.3099}, {120., 18.3099}};
Interpolation[data]

but for some reason it does not Interpolated correctly. If I plot the data it looks fine. Can someone tell me why Interpolation doesn't correctly fit this data?

I get the following errro message:

InterpolatingFunction::dmval: Input value {0.00245143} lies outside the range of data in the interpolating function. Extrapolation will be used.

Probably has something to do with the error message, no? Or you don't get one? — Michael E2, Nov 22 '20 at 01:15
@MichaelE2 yes! I just updated the question for you to see the error that I get — John, Nov 22 '20 at 01:16
Hmm, I get "Interpolation::inddp: The point 70.6564` in dimension 1 is duplicated." — Michael E2, Nov 22 '20 at 01:17
I was getting that too before. But the problem is that I don't really see any problem with the data that will make interpolation not to work — John, Nov 22 '20 at 01:19
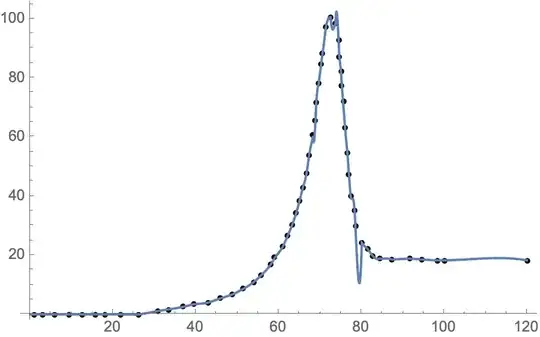
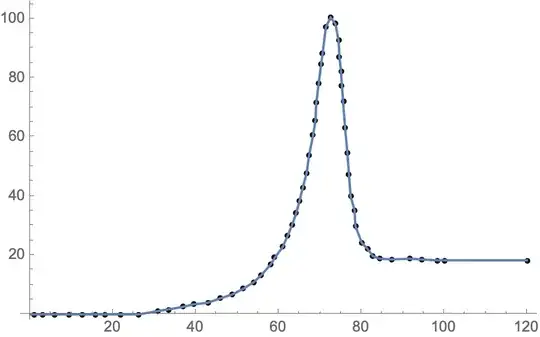
To answer the question about your error message, show the code that produced it. Mine could be due to the code for data being incomplete (the numbers are rounded to six digits). One can see by eye that there are two points with 70.6564 in the first coordinate. — Michael E2, Nov 22 '20 at 01:19
Above is exactly as I put it. I just put Interpolation[data]. If you put ListLinePlot[data] you can see that the data plots very different than the interpolation function fitting — John, Nov 22 '20 at 01:23
Sometimes Mathematica error messages are inscrutable, but here both are clear. Interpolation::inddp: The point 70.6564 in dimension 1 is duplicated. means you have two values for 70.6564 in data. Either nudge one by a small amount or drop one. InterpolatingFunction::dmval: Input value {0.00245143} lies outside the range of data in the interpolating function. Extrapolation will be used. is more a warning than an error: your data start at 0.965251 so when you ask for 0.00245143, Mathematica needs to extrapolate. It might work out fine, it might be catastrophically wrong. — Chris K, Nov 22 '20 at 01:23
@ChrisK how can I fix it then? I have tried removing one of the values with 70.6564 and it still does not fit it correctly or similar to when you plot the data. — John, Nov 22 '20 at 01:25

Chris K · Accepted Answer · 2020-11-22T01:35:53.143

5

This is what happens when I drop the second value for 70.6564.

Show[
 ListPlot[data, PlotStyle -> Black],
 Plot[Evaluate@Interpolation[data][x], {x, 0, 120}, PlotRange -> All]
]

If those wiggles bother you, use linear interpolation instead:

Show[
 ListPlot[data, PlotStyle -> Black],
 Plot[Evaluate@Interpolation[data, InterpolationOrder -> 1][x], {x, 0, 120}, PlotRange -> All]
 ]

Or if you don't need the InterpolatingFunction to go exactly through the data, try this approach to regularised Interpolation.

edited Nov 22 '20 at 01:35

answered Nov 22 '20 at 01:28

Chris K

20,207
3
39
74

1

Awesome! Christ thank you very much for your suggestion and also about the wiggles! This is what I wanted! I really appreciate it – John Nov 22 '20 at 01:35

Interpolation not working

1 Answers1