Numerical solution of an iterative equation

Question

I am trying to solve the following iterative equation:

where the parameter tao (needed in the previous equation) is defined as:

Here's the parameters and my approach to solving the equation in Mathematica:

ah = 342496; (*J/mol*)
R = 8.314; (*J/mol.K*)
A = 7.6*10^-38; (*s*)
b = 0.67;
x = 0.49;
q = -0.1/60;(*K/s*)
T0 = 500;(*K*)
Tfinal = 350;(*K*)
dt = 0.1 ;(*s*)
n = (T0 - Tfinal)/dt; (*number of steps*)
Tf0 = T0;
dT = dt*q; (*K*)

Tk = T0 + Sum[dT, {i, 1, n}]; 
τ = A*Exp[(x ah)/(R Tk) + (1 - x) (ah/Subscript[T, fkminus1])]; 
Tf = T0 + Sum[dT (1 - Exp[-Sum[(dT/(q*τ))^b, {i, 1, n}]]), {i, 1, n}]

In the code, notice that dT = dt*q, where dt is a time step that I choose which ideally should be small enough as to ensure that Tf decays less than 1 K. Also, notice that $\tau_{0,k}$ is a function of $T_{f,k-1}$ ($T_{f,0}$ is defined in the code as 500) and $T_k$.

The problem I am having is that I do not know how to connect the two equations so that the $T_k$ that I calculate from equation 1, eventully goes to equation 2 and the $\tau_k$ that I calculate from equation 2 goes to equation 1.

Questions

How can I solve the Tf equation?
How can I plot Tf vs T, similar to the figure below (only for one q, in this case for q = -0.1/60)?. Notice that the parameters from figure below are the same I am using in the code.

Note: Here's the paper where the two equations are coming from as well as the figure (figure 1 in that paper) in case anybody wants to look at it: https://sci-hub.se/10.1016/s0260-8774(02)00212-1.

I hope everything is clear and I appreciate in advance your help.

EDIT: Clarification on the parameters

ΔT is the change in temperature and it is related by the change in time (which is set by the user, small enough so that Tf doesn't decrease more than 1 K) as ΔT=dt*q. Both, dt and q can be taken as constant. ΔTk represents then a series of temperature steps.
qk is the cooling rate in Kelvin/seconds at which the process is performed. In the code it fixed with value of -0.1/60 (or -0.0016 Kelvin/second). The negative sign is because it is a cooling process (it would be positive if it was heating).
T,k is simply the temperature, which is defined as Tk = T0 + Sum[dT, {i, 1, n}], where T0 is the initial temperature of the process and is 500 (kelvin).
Δh is an apparent activation energy in J/mol
tao,k (from equation 20) is the relaxation time and it is a function of Tf,k-1 (The initial Tf(0)=500) and Tk
Tf,k which is what I want to calculate can be considered to be as the "glass transition temperature". Hence, it depends on the material and it is quite different than T,k which is just the process temperature.

So, as you can see, every parameter is known except Tf which is what I want to solve by doing this numerical method given the known parameters.

At time zero, for example

tao = A*Exp[((x*ah)/(R*Tk)) + ((1 - x)*ah/Subscript[T, fkminus1])] = 
   7.6*10^-38*
    Exp[((0.49*342496)/(8.314*499.75)) + ((1 - 0.49)*342496/500)];

and then with the above tao we use it to calculate Tf at time 0 and then you can calculate tao at the next time, which allows you to calculate 'Tf' and the same time. The process repeats in an iterative way (which I don't know how to do in Mathematica) until we are able to plot for instance Tf vs T for a set of T. The set of T in this case goes from 500 to 350 (to be able to plot as in the figure). Notice that because the temperature set is already fixed between 500 and 350, the number of steps n is simply n = (T0 - Tfinal)/dt

I think you could envision your formulae as definitions rather than equations to be solved simultaneously. You will need to set up an iterative process, calculating e.g. $\tau_{0,k}$ using $T_{f,k-1}$, i.e. the value obtained from the previous step, then using those values to calculate the next $T_{f,n+1}$. You may be interested in the original paper by Hodge and Berens where this model was introduced; it goes into (a little) more detail on the significance of the parameters as well. — MarcoB, Nov 25 '20 at 03:13
@MarcoB thank you very much. I had no idea you also knew about the Hodge and Berens paper!. Do you know about the area?. Yes, the seminal work of the Hodge paper goes a little bit more into detail but the equations from the paper I put are the same and a little bit easier to understand in notation. You are right that this is an iterative process in which the number of steps are set by selecting an appropiate step of time. The problem I am having the most if how to implement this iterative process. I though just by simply using the "summation" was enough but I am struggling to connect both eqs. — John, Nov 25 '20 at 03:18
Your formula $(19)$ needs further explanation. Is the $j$ indexing used inside the inner summation? — Cesareo, Nov 26 '20 at 11:18
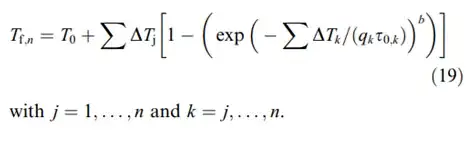
@Cesareo the j indexing is for the first "Delta T". Also notice that in this case j and k are the same (when j=1, k=1 and so on.). The indexing matters the most in equation 20, where the indexing of Tf is with k-1. I hope this is clear. — John, Nov 26 '20 at 19:51
What are $\Delta T_j$, $T_k$, $\Delta T_k$, $q_k$, $\Delta h$? Some of quantities appear to be functions of an integer variable, variously $j,k,n$, but your code shows no such dependency, different names for some variables (maybe?). You say "solve the...equation," but it looks like a fairly straightforward iterative calculation: Is that correct or do you want to solve for an unknown? You might get more help if you made it easier to understand. — Michael E2, Nov 26 '20 at 21:28
@MichaelE2 I have added an update in the question to answer your question and be more clear on the meaning of each parameter and also on the unknown. It is actually a fairly straightforward iteration process which I do not know how to implement in Mathematica. It pretty much consist in calculating tao at time 0 which allows you to calculate Tf (which is what I want) at time 0 which in turn allows you to calculate tao at the following time and this in turn allows you to calculate Tf at the next following time and so.... Let me know if you need any further clarification — John, Nov 26 '20 at 22:06
@MichaelE2 yes, T,k is a process temperature (for example if I heat soap in an oven, it will be the temperature I set the oven) while Tf,k is formally known as the "fictive temperature" and can be regarded as being similar to the "glass transition temperature" or the temperature at which a material goes from a hard to a glassy solid (hence it depends on the material or in the soap example where the soap will change to another state to due to process temperature). I hope that's clear and let me know if you have any other quesiton — John, Nov 27 '20 at 02:05

Alex Trounev · Accepted Answer · 2020-11-29T13:37:39.433

Solution for one set of parameters with cooling is very simple, but for the case of heating we need some small modification of code. Code for cooling case:

ah = 342496;(*J/mol*)R = 8.314;(*J/mol.K*)A = 7.6*10^-38;(*s*)b = 0.67;
x = 0.49;
q = -0.1/60;(*K/s*)T0 = 500;(*K*)Tfinal = 350;(*K*)dt = 300;(*s*)n = 
 IntegerPart[Abs[(T0 - Tfinal)/dt/q]];(*number of steps*)Tf0 = T0;
dT = dt*q;(*K*)T[k_] := T0 + Sum[dT, {i, 1, k}];
tf[0] = T0; Do[
 tau[k] = AExp[(x ah)/(R T[k]) + (1 - x) ah/(R tf[k - 1])]; 
 tf[k] = T0 + 
Sum[dT (1 - Exp[-(Sum[dT/(qtau[j]), {j, i, k}])^b]), {i, 1, k}];, {k, n}]

Visualization

Tfc = Table[{T[k], tf[k]}, {k, n}]; 
T[0] = T0; cp = 
 Table[{T[k], (tf[k] - tf[k - 1])/(T[k] - T[k - 1])}, {k, n}];
{ListPlot[Tfc, PlotRange -> All, AxesLabel -> {"T", "Tf"}], 
 ListPlot[cp, PlotRange -> All, AxesLabel -> {"T", "cp"}]}

Note, that even for dt = 300 we have 300 points for numerical solution. If we put dt=.1 as proposed, then it goes to 9*10^5. It takes a time to calculate this process with small steps. Heating compare to cooling is quite tricky since equation of heating is not shown in a paper linked. First, we put

Tf0 = tf[n];q = 0.1/60;(*K/s*)T0 = 350;(*K*)Tfinal = 500;(*K*)dt = 300;(*s*)n1 = 
 IntegerPart[Abs[(T0 - Tfinal)/dt/q]];(*number of steps*)
dT = dt*q;(*K*)T1[k_] := T0 + Sum[dT, {i, 1, k}];

Second, we use

tf1[-1] = Tf0; T1[0] = T0;
tau[0] = AExp[(x ah)/(R T0) + (1 - x) ah/(R Tf0)]; Do[
 tau[k] = AExp[(x ah)/(R T1[k]) + (1 - x) ah/(R tf1[k - 1])]; 
 tf1[k] = Tf0 + 
   Sum[dT (1 - Exp[-(Sum[dT/(q*tau[j]), {j, 0, i}])^b]), {i, 0, 
     k}];, {k, 0, n1}]

Visualization

Tfh = Table[{T1[k], tf1[k]}, {k, n1}]; cp1 = 
 Table[{T1[k], (tf1[k] - tf1[k - 1])/(T1[k] - T1[k - 1])}, {k, n1}];
{ListPlot[{Tfc, Tfh}, AxesLabel -> {"T", "Tf"}, PlotLegends -> {"Cooling", "Heating"}, PlotStyle -> {Blue, Red}], 
 ListPlot[{cp, cp1}, AxesLabel -> {"T", "cp"}, 
  PlotLegends -> {"Cooling", "Heating"}, PlotStyle -> {Blue, Red}]}

Alex Trounev, thank you very much. The code looks very good!. If it is not too much trouble how can the code be modified for the heating case to plot the Tf vs T and the Cp vs T of any of the heating cases of the paper?. I am accepting your answer and giving you the 100 points. I really appreaciate your help very much ! — John, Nov 28 '20 at 01:16
@John I have uploaded code for heating glass, but result is not exactly what they shown in a paper. — Alex Trounev, Nov 28 '20 at 18:10
Alex Trounev thank you for your effort. Yes, its weird because the only difference between the cooling and heating formula is the negative sign in q and the fact that now it goes from T0 (350) to Tfinal(500), rather than the other way around as on cooling. Anyways, I appreciate very much your effort ! — John, Nov 28 '20 at 20:55
Alex now that you ask perhaps one more. Is it possible to easily modify your code for different cooling and heating rates?. Similar to the paper where they do it for several rates. I tried doing it but it seems that it is necessary to modify dt every time because for some rates dt needs to be smaller. How can I do this? — John, Nov 28 '20 at 21:53
@John We can use fixed n=300 and put dT=(Tfinal-T0)/n for any q (as they did in a paper). For cooling dT<0 and for heating dT>0. — Alex Trounev, Nov 28 '20 at 22:14

score 3 · Answer 2 · answered Nov 29 '20 at 17:09

I read Your question carefully.

(A) You give a value $q$ and your image gives values $q_k$ with $k={c,h}$. OK. That is cold and hot. But q changes from right to left an back. It is constant and has to be modelled.

(B) All functions start parallel to the x-axis up to $T_{initial}$ somewhat below $T=400K$. It is not logical to have something on a temperature much higher than the univariate temperature.

(C) q is in thermodynamics a known symbol. Conduct this search for references: thermodynamics symbol q. That is heat not temperature. Do not mix that up.

(D) The thick black line seems of key interest to the graph. I suggest use how to make a curve selectable from a scaned image and convert it to a list of coordinates/ like this

and solve for some $f(T)$ which includes the $q$ and other influences.

(E) By this method You can infer the second asymptote letting all measures curves head to ${T_{x-axis},T_{f}}={500 K,500 K}$. This type of common upper hold or asymptotic common temperature unifies the approaches.

(F) The heated branches and the cooling branches are not to clear from the image. Just for one pair of branches arrows are inserted. The three other can not be infered but guessed or known from elsewhere.

(G) Experts will not be too satisfied with this image.

(H) Use for a better readability of Your personal input mathjax basic tutorial and quick reference.

(I) As alex-trounev showed nicely there is no such "knee" from the given formulae. This really swings back to the asymptote:

i = Binarize@img; i1 = Binarize[Show[i, g[{White, Disk[#, disk] & /@ vxPos}]]]; i2 = ColorNegate@Erosion[i1, 1]; ...

(J) For some better theory search the internet or accept my advise with this publication Nature, Scientific reports Heat flow due to time-delayed feedback by Sarah A. M. Loss and Sabine H. L. Klapp in Scientific Reports volume 9, Article number: 2491 (2019). Especially Figure 2 seems relevant to a solution. There of course many other probably closer related scientific texts out there on heat flow with a time delay feedback. The special point seems to me that the first asymptotic holds in this experiment might be by design of the experiment.

(K) The intent of the author seems to me the transistion from direct following the controlled heat inflow to this delayed behaviour. So both can not be modelled with the same mathematical methodologies.

Numerical solution of an iterative equation

2 Answers2

Linked