I would like to gain some knowledge about how to transform differential operators to different coordinate systems using Mathematica. I know that the Laplacian command has an optional parameter chart that does this for various coordinate systems but I would like to gain some insight and possibly intermediate solutions doing this. As a simple test example, I believe the laplacian in polar coordinates will do just fine. So, I would like to transform
$$
\Delta u = u_{xx} + u_{yy}
$$
using $u(x,y)=w(r,\phi)$ and the transformation $x=r \cos\phi, y=r\sin\phi$ into
$$ \Delta w = \color{red}{\frac{1}{r^2}}w_{rr} + \frac{1}{r}w_{r} + \frac{1}{r^2} w_{\phi\phi} $$
Without incorporating the specific transformation one can of course calculate
D[w[r[x, y], phi[x, y]], x, x] + D[w[r[x, y], phi[x, y]], y, y]
but how would you use the transformation from here? How would you do this in a "step by step" manner, e.g. how would you calculate the derivative(s) of $r$ w.r.t. $x$?
Edit: as was kindly pointed out by Daniel Huber, the red part in the above laplacian shouldn‘t be there.

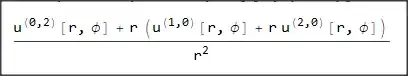
DChangefrom hisMoreCalculusreally helps (unless I'm misusing it). I triedDChange[w = Laplacian[u[x, y], {x, y}], "Cartesian" -> "Polar", {x, y}, {r, \[Theta]}, {}]and the result was uninformative, keeping intact the formDerivative[0, 2][u][r*Cos[\[Theta]], r*Sin[\[Theta]]] + Derivative[2, 0][u][r*Cos[\[Theta]], r*Sin[\[Theta]]]and just stating the forms ofrand\[Theta]in terms ofxandy(along with the list of obvious restrictions onrand\[Theta]. – murray Nov 25 '20 at 18:11TransformedField["Cartesian" -> "Polar", Laplacian[u[x, y], {x, y}], {x, y} -> {r, \[Theta]}]just returns\!\(\*SuperscriptBox[\(u\), TagBox[ RowBox[{"(", RowBox[{"0", ",", "2"}], ")"}], Derivative], MultilineFunction->None]\)[r Cos[\[Theta]], r Sin[\[Theta]]] + \!\(\*SuperscriptBox[\(u\), TagBox[ RowBox[{"(", RowBox[{"2", ",", "0"}], ")"}], Derivative], MultilineFunction->None]\)[r Cos[\[Theta]], r Sin[\[Theta]]]. – murray Nov 25 '20 at 18:13