Find coefficients of a periodic function with non-linear fit

Question

Description of the problem:

I'm studying a signal that is the sum of two exponentials at two different frequencies:

$z(n) = A_1*e^{2\pi i\nu_1n } + A_2*e^{2\pi i\nu_2 n } + noise$

The signal itself is known because all the parameters $\nu_1$, $\nu_2$, $A_1$ and $A_2$ are defined at the beginning of the code and I evaluate the signal for integer values of $n$ and the noise is also well defined. I can compute the analytical expression of the Fourier coefficients of my signal.

What I would like to do is to retrieve the two frequencies ($\nu_1$ and $\nu_2$) and the two amplitudes ($A_1$ and $A_2$) of the original signal using a non-linear fit on the analytical expression of the Fourier coefficients. So far, my fit is working well and I'm able to get the correct value of the frequencies with an error of $\approx 1e-7$ but the values of the amplitudes is well far from being correct. I've already tried to change the initial value and to not put any initial guess for the coefficients but they always converge to the same value.

I implemented the fit in this way:

nlm = 
  NonlinearModelFit[
    DataForFit, ModelForFit {indPeak}, {{C1, 0.5}, {C2, 0.5}, {q1, tune1FFT}, 
    {q2, tune2FFT}}, indPeak, 
    MaxIterations -> Infinity]

Where the function ModelForFit is:

ModelForFit =  Abs[C1 * Sinc[\[Pi]* NN[[5]]*(q1 -  indPeak/ NN[[5]])]/
      Sinc[\[Pi]*(q1 -  indPeak/ NN[[5]])]* NN[[5]]*Exp[\[Pi]*I*( NN[[5]] - 1)*(q1 -  indPeak/ NN[[5]])] + C2* Sinc[\[Pi]* NN[[5]]*(q2 -  indPeak/ NN[[5]])]/Sinc[\[Pi]*(q2 -  indPeak/ NN[[5]])]* NN[[5]]*
     Exp[\[Pi]*I*( NN[[5]] - 1)*(q2 -  indPeak/ NN[[5]])] ];

And $N$ is the maximum value of $n$

EDIT : FULL CODE

    HSignal = A1*Exp[2*\[Pi]*I*\[Nu]1*n ] + A2*Exp[2*\[Pi]*I*\[Nu]2*n ] + Sum [Exp[2*\[Pi]*I*\[Nu]1*n *k - k], {k, 1, 4}] + Sum [Exp[2*\[Pi]*I*\[Nu]2*n *k - k], {k, 1, 4}];
A1 = 0.73;
A2 = 0.15;
\[Nu]1 = 0.1180;
\[Nu]2 = 0.4142;
NN = NumericArray[{32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 
   16384}, "Integer16"]; (*Comment: any value of this vector can be used, here below I picked NN[[5]], but you can pick any other position*)
xx = Range[0, NN[[10]] - 1, 1];
NumericalFFT = Fourier[{HSignal /. n -> xx}, FourierParameters -> {1, -1}];
phi = Abs[NumericalFFT];
phiModifiedShape = phi[[1]]; peaks = FindPeaks[phiModifiedShape]; Print[peaks];
OrderedPeaks = ReverseSortBy[peaks, Last] // MatrixForm;
Print[OrderedPeaks];
ind1 = OrderedPeaks[[1, 1]]; ind2 = OrderedPeaks[[1, 2]];
Print["First peak identification: ", ind1[[1]], 
  ". Second peak identification: ", ind2[[1]]];
tune1FFT = N[(ind1[[1]] - 1)/NN[[5]]]; tune2FFT = 
 N[(ind2[[1]] - 1)/NN[[5]]];
Print["Tunes from FFT: ", tune1FFT, "  ", tune2FFT];
XForFit = {ind1[[1]] - 1, ind1[[1]], ind1[[1]] + 1, ind2[[1]] - 1, 
ind2[[1]], ind2[[1]] + 1};
YForFit = phiModifiedShape[[XForFit]];
DataForFit = Transpose[{XForFit, YForFit}];
ModelForFit = (find it above)
nlm = (find it above)
Print[nlm["ParameterTable"]];

In my model $\nu_1$, $\nu_2$, $A_1$ and $A_2$ are respectively replaced by q1, q2, C1, C2.

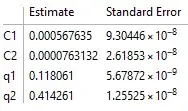
As you can see the errors on the 4 parameters are quite small. But while the values of the frequency is correct, the value of the amplitude is wrong (it was supposed to be (0.73 and 0.15).

Question:

Therefore,

1. Which is the method that Mathematica uses to perform the fit? On the documentation I read that in absence of any specification it will be picked automatically, but I wasn't able to understand how it makes this choice and which one it picks.
2. Do you have any suggestion on how to improve the estimation of the coefficients? In general, I'm able to give to the model a value that is not too far (but at the same time not too close) to the real one.

I hope my questions and the problem are clear enough!