How to unite polygons of the same color into a single polygon?

Question

Let a partition of a planar polygon into colored polygons be given, i.e. something similar to

We know the coordinates of the vertices and the color of each part, e. g. in such a way

Graphics[{EdgeForm[Black], Red,  Polygon[{{0, 0}, {0, 2}, {2, 2}, {2, 1}, 
    {3, 1}, {3, 2}, {4, 2}, {4, 0}}], 
 EdgeForm[Black], Green,    Polygon[{{0, 2}, {0, 6}, {3, 6}, {3, 4}, {2, 4}, 
    {2, 5}, {1, 5}, {1, 3}, {2, 3}, {2, 2}}], 
 EdgeForm[Black], Blue, Polygon[{{1, 3}, {1, 5}, {2, 5}, {2, 3}}], 
 EdgeForm[Black], Red, Polygon[{{3, 2}, {3, 6}, {5, 6}, {5, 2}}],
 EdgeForm[Black], Green, Polygon[{{2, 1}, {2, 4}, {3, 4}, {3, 1}}], 
 EdgeForm[Black], Green, Polygon[{{4, 0}, {4, 2}, {5, 2}, {5, 0}}]}]

How to write a Mathematica program which unites the polygons having a joint edge and the same color into a single polygon with the simply-connected interior, not a polygonial figure (see Encyclopedia of Mathematics and Wiki)? For the above partition we have to obtain two green polygons, one red polygon, one yellow polygon, one blue polygon, and one violet polygon.

Addition. The following result in green is not a polygon so is not allowed:

Answer 1

Input examples

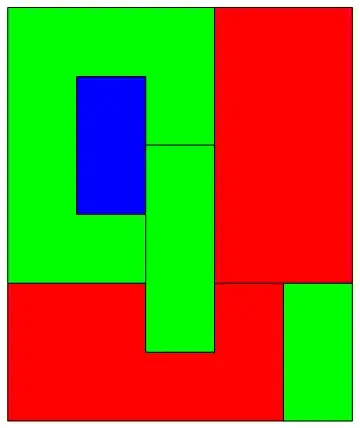
First a slightly modified form of the example input from OP:

gr1 = Graphics[SequenceReplace[#, p : {_RGBColor, _Polygon} :> p] & @
   {EdgeForm[ Black], Red, Polygon[{{0, 0}, {0, 2}, {2, 2}, {2, 1}, {3, 1}, {3, 2}, 
       {4, 2}, {4, 0}}], 
  EdgeForm[Black], Green, Polygon[{{0, 2}, {0, 6}, {3, 6}, {3, 4}, {2, 4}, {2, 5}, 
       {1, 5}, {1, 3}, {2, 3}, {2, 2}}], 
  EdgeForm[Black], Blue, Polygon[{{1, 3}, {1, 5}, {2, 5}, {2, 3}}],
  EdgeForm[Black], Red,  Polygon[{{3, 2}, {3, 6}, {5, 6}, {5, 2}}], 
  EdgeForm[Black], Green, Polygon[{{2, 1}, {2, 4}, {3, 4}, {3, 1}}]}];

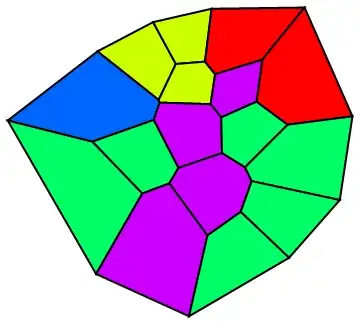
Additional examples where the combined regions have no holes (gr2) , a single hole (gr3) and multiple holes (gr4):

SeedRandom[1]
polygons = MeshPrimitives[VoronoiMesh[RandomReal[{-1, 1}, {20, 2}]], {2, "Interior"}];
{gr2, gr3} = Graphics[{EdgeForm[{Thick, Gray}], 
      MapIndexed[Function[{x, y}, Table[{ColorData[{"Rainbow", {1, Length@#}}]@y[[1]], 
          polygons[[i]]}, {i, x}]], #]}] & /@ 
       {{{2, 5, 10}, {3, 6}, {4, 8}, {1, 7}, {9}}, 
       {{5, 10, 9, 7, 3}, {6}, {4, 8}, {2, 1}}};
SeedRandom[77]
gr4 = Graphics[{EdgeForm[Gray], {RandomChoice[{2, 1} -> {Red, Blue}], #}} & /@ 
    MeshPrimitives[MengerMesh[2], 2]];
Grid[{Style[#, 24] & /@ {"gr1", "gr2", "gr3", "gr4"}, 
  Show[#, ImageSize -> 250] & /@ {gr1, gr2, gr3, gr4}}, 
 Dividers -> All]

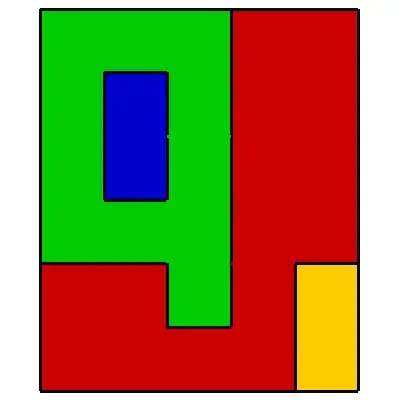
Combined polygons allowed to have holes:

We group polygons by color and take the RegionUnion of each group of polygons and RegionPlot it with the color associated with the group:

ClearAll[bdR, combinePolygonsByColorHolesAllowed]
bdR = BoundaryDiscretizeRegion[RegionUnion @@ #, 
    MeshCellStyle -> {2 -> #2, 1 -> Directive[Thick, Gray]}] &;
combinePolygonsByColorHolesAllowed = Show[Values[
     GroupBy[Cases[#[[1]], {_RGBColor, _Polygon}, All], First, 
      Module[{color = #[[1, 1]], polys = #[[All, 2]]}, 
        bdR[polys, color]] &]], PlotRange -> All, Frame -> False, 
    AspectRatio -> Automatic] &;
Grid[{Style[#, 24] & /@ {"gr1", "gr2", "gr3", "gr4"}, 
    Show[#, ImageSize -> 250] & /@ #, 
    Show[#, ImageSize -> 250] & /@ combinePolygonsByColorHolesAllowed /@ #}, 
   Dividers -> All] &@{gr1, gr2, gr3, gr4}

Combined polygons cannot have holes:

If holes are not allowed, we need to identify the holes in the region formed by the group of polygons. For this purpose, we BoundaryDiscretizeRegion the RegionUnion of the polygon group and use the (undocumented) function Region`Mesh`FindMeshRegionHoles which returns None if the mesh region does not have any holes and, if it does, a point for each of the holes. For each hole h, we find the polygons that lie on the line from a point in h to nearest point on the outer boundary (obtained using ConnectedMeshComponents) and BoundaryDiscretizeRegion the RegionUnion of resulting partition of the polygon group.

ClearAll[findHoles, combinePolygonsByColorNoHoles]
findHoles = RegionMeshFindMeshRegionHoles[
  BoundaryDiscretizeRegion[RegionUnion @@ #]] &;
combinePolygonsByColorNoHoles = Show[Values[
     GroupBy[Cases[#[[1]], {_RGBColor, _Polygon}, All], First, 
      Module[{color = #[[1, 1]], polys = #[[All, 2]], 
         bdr = BoundaryDiscretizeRegion[RegionUnion @@ #[[All, 2]]], 
         outerboundary,  lines, partition},
        If[findHoles[polys] === None, bdR[polys, color], 
         outerboundary =  First@ConnectedMeshComponents[
            DiscretizeGraphics[MeshPrimitives[bdr, {1, "Boundary"}]]];
         lines =  Rationalize[Line[{#, RegionNearest[outerboundary, #]}] & /@ 
            findHoles[polys], 10^-4]; 
         partition = {Complement[polys, ##], ##} & @@ 
           Table[Select[Rationalize[polys, 10^-4], 
             Head[RegionIntersection[#, ln]] === Line &], {ln , lines}]; 
         Show[bdR[First @ partition, color], 
          bdR[#, Lighter @ Lighter @ color] & /@ Rest[partition], 
          PlotRange -> All]]] &]],
     PlotRange -> All, Frame -> False, AspectRatio -> Automatic] &;

Showing input graphics (first row), outputs from combinePolygonsByColorHolesAllowed (second row) and outputs from combinePolygonsByColorNoHoles (third row):

Grid[{Style[#, 24] & /@ {"gr1", "gr2", "gr3", "gr4"}, 
    Show[#, ImageSize -> 250] & /@ #, 
    Show[#, ImageSize -> 250] & /@ combinePolygonsByColorHolesAllowed /@ #, 
    Show[#, ImageSize -> 250] & /@ combinePolygonsByColorNoHoles /@ #}, 
 Dividers -> All] & @ {gr1, gr2, gr3, gr4}

Focusing on the red polygons in gr4:

gr4a = Graphics[{EdgeForm[Gray], Cases[gr4[[1]], {Red, _}, All]}, 
   ImageSize -> Medium];
gr4b = Replace[combinePolygonsByColorHolesAllowed[gr4], 
  {Directive[{___, Blue, ___}], _} -> {}, All];
gr4c = Replace[combinePolygonsByColorNoHoles[gr4],
  {Directive[{___, Blue | Lighter[Lighter@Blue], ___}], _} -> {}, All];
Row[Show[#, ImageSize -> 250] & /@ {gr4, gr4a, gr4b, gr4c}]

Note: We can also use RegionPlot instead of BoundaryDiscretizeRegion above; that is, we can replace the function rdF above with rP:

rP = RegionPlot[RegionUnion @@ #, PlotPoints -> 90, 
    MaxRecursion -> 5, PlotStyle -> #2, BoundaryStyle -> Thick] &;

The 2D primitives produced by the functions above are FilledCurves if we use rdF; they are Polygons if we use rP.