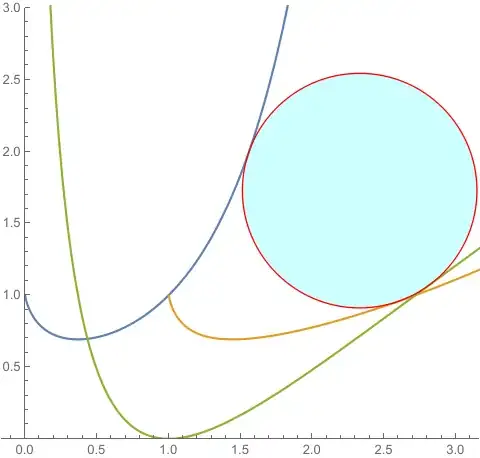
f[x_] := x^x
g[x_] := Log[x]^Log[x]
h[x_] := Log[x]^2
plot = Plot[{f[x], g[x], h[x]}, {x, 0, E}, PlotRange -> {0, 1}]

Extract the three lines from plot and use them to construct three RegionDistance functions:
{linef, lineg, lineh} = Cases[plot, _Line, All];
{rdf, rdg, rdh} = RegionDistance /@ {linef, lineg, lineh};
ContourPlot to get the lines where rdf[{x, y}] == rdh[{x, y}] and rdg[{x, y}] == rdh[{x, y}]:
cp = ContourPlot[{ConditionalExpression[rdf[{x, y}] - rdh[{x, y}],
y <= f[x]] == 0, rdg[{x, y}] - rdh[{x, y}] == 0},
{x, 0.434, 2.5}, {y, 0, 1}, ContourStyle -> {Red, Green}];
Show[plot, cp]
Find the intersection of the two contour lines:
center = First @ Graphics`Mesh`FindIntersections @ cp
{0.912936, 0.468359}
The distances to the three curves are
Through[{rdf, rdg, rdh} @ center]
{0.374443, 0.374455, 0.374516}
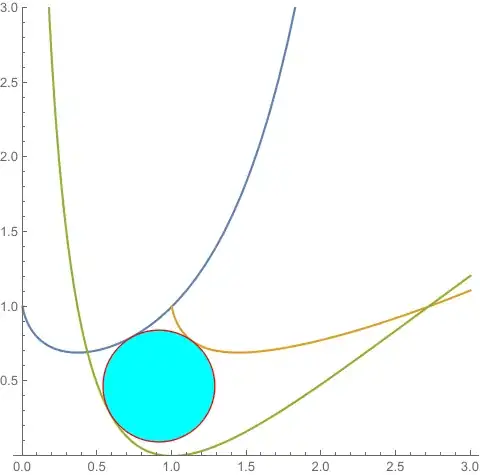
Display the curves with the circle found, points of tangency and normals:
{ptf, ptg, pth} = RegionNearest[#, center] & /@ {linef, lineg, lineh};
Show[plot, Graphics[{AbsolutePointSize[10], Thick,
Red, Circle[intersection, rdf@center],
Dashed, ColorData[97]@1,
InfiniteLine[{ptf, ptf + Cross @ {1, f'[ptf[[1]]]}}],
ColorData[97]@2, InfiniteLine[{ptg, ptg + Cross @ {1, g'[ptg[[1]]]}}],
ColorData[97]@3, InfiniteLine[{pth, pth + Cross @ {1, h'[pth[[1]]]}}],
Black, Point@intersection, Black, Point @ {ptf, ptg, pth}}],
AspectRatio -> Automatic, ImageSize -> 700]

A slower alternative: extract the two contourlines and find their intersection using RegionIntersection:
edlines = Cases[Normal @ cp, _Line, All];
center = (RegionIntersection @@ edlines)[[1, 1]]
{0.912936, 0.468359}
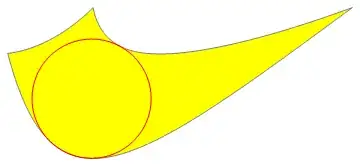
An aside: To find the largest circle enclosed within the region (without the constraint that the circle touches all three curves) we can do
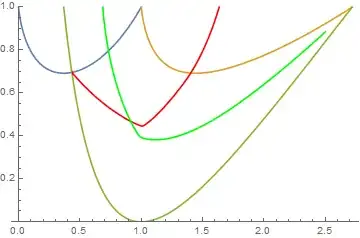
pw[x_] := Piecewise[{{f[x], x <= 1}}, g[x]];
plot = Plot[{f[x], g[x], h[x], pw[x], Min[pw[x], h[x]]}, {x, 0, E},
Exclusions -> None, PlotRange -> {0, 1},
Filling -> {4 -> {{3}, {None, Yellow}}}]

Extract the polygon from plot:
poly = First @ Cases[Normal[plot], _Polygon, All];
Use SignedRegionDistance with poly to get an objective function to be used with NMinimize:
srd[{x_, y_}]:= SignedRegionDistance[poly][{x, y}]
Find the coordinates within poly that maximizes the distance to the boundary of poly:
sol = NMinimize[{srd[{x, y}], {x, y} ∈ poly}, {x, y}]
{-0.394924,{x->0.991457,y->0.395402}}
Process to get the radius and center of largest circle within poly:
{radius, center} = {Abs @ #, {x, y} /. #2} & @@ sol
{0.394924,{0.991457,0.395402}}
Display:
Graphics[{EdgeForm[Gray], Yellow, poly, Red, Circle[center, radius]}]
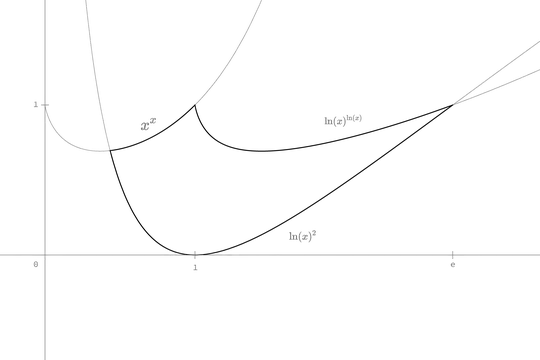 I think that one way is to find two equidistance curves. Let's say $E_1$ the equidistance curve between $f(x)$ and $h(x)$, and $E_2$ the equidistance curve between $g(x)$ and $h(x)$. Then the point of intersection between $E_1$ and $E_2$ would be $C$ at the same Euclidean distance from the three curves.
I think that one way is to find two equidistance curves. Let's say $E_1$ the equidistance curve between $f(x)$ and $h(x)$, and $E_2$ the equidistance curve between $g(x)$ and $h(x)$. Then the point of intersection between $E_1$ and $E_2$ would be $C$ at the same Euclidean distance from the three curves.