Drawing hollow disks in 3D with an sphere in center and small spheres on the rings

Question

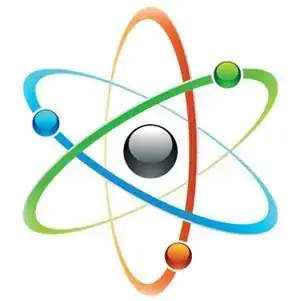
I was trying to draw the following logo of an atom using Mathematica, but I could only figure out how to draw intersecting ellipses, not a nice logo like below. Do you have any idea? And is Mathematica a good option for this work or I should look for a drawing sofware?

Note that the image is an artist rendering. I don't think it actually corresponds to a 3D-symmetric spatial configuration. (E.g. the "triangle" in front of the sphere should be bigger than the triangle behind it.) — Michael E2, Dec 09 '20 at 18:11
@MichaelE2 One could interpret it as being the limit as one takes dolly-out, zoom-in to infinity. — Acccumulation, Dec 10 '20 at 19:02
@Acccumulation Almost. The crossings aren't correct, unless the orbits are of different radii, in which case they'd appear to be different sizes. If the thickness was the same throughout the orbit, the thickness wouldn't vary front to back from a perspective infinitely far away. — Michael E2, Dec 10 '20 at 19:18

Michael E2 · Accepted Answer · 2020-12-09T21:44:33.500

Bells and whistles. Doesn't replicate the crossings of the orbits in the artwork, but it's more consistent. Colors and lighting are a bit hard to get right.

ClearAll[orbit];
orbit // Options = {ColorFunction -> None};
orbit[OptionsPattern[]] :=
  With[{cf = OptionValue[ColorFunction],
    rot = ( {
       {1, 0, 1/10},
       {0, 1, 1/10}
      } )}, 
   Polygon[CirclePoints[1., 120].DiagonalMatrix[{0.3, 1.}].rot -> 
     CirclePoints[{-0.07, 0.}, 0.82, 
       120].DiagonalMatrix[{0.3, 1.1}].rot, 
    VertexColors -> (cf /. {None | Automatic -> Automatic, 
        f_ :> f /@ (Range[120]/120.)})]
   ];
paths = With[{sph = 0.85 {Cos[-0.85] + 0.05, Sin[-0.85]} {0.3, 1.1}},
  Graphics3D[{
    EdgeForm[{Thickness@Medium, White}]
    , {orbit[ColorFunction ->
       (Blend[{Hue[0.05, 1, 0.8], Darker[Yellow, 0.1]}, 
          Cos[Pi # + Pi/4]^2] &)]}
    , GeometricTransformation[
     {orbit[ColorFunction ->
        (Blend[{Hue[0.55, 0.9, 0.7], Darker[Cyan, 0.1]}, 
           Cos[Pi # + Pi/4]^2] &)]},
     RotationTransform[-2 Pi/3, {0, 0, 1}]
     ]
    , GeometricTransformation[
     {orbit[ColorFunction ->
        (Blend[{Darker[Green, 0.4], Darker[Yellow, 0.2]}, 
           Cos[Pi # + Pi/4]^2] &)]},
     RotationTransform[2 Pi/3, {0, 0, 1}]
     ]
    }, PlotRange -> 1, PlotRangePadding -> Scaled[.05], 
   ViewPoint -> Top, Boxed -> False, Lighting -> "Neutral"]
  ];
spheres = With[{sph = 0.85 {Cos[-0.85] + 0.05, Sin[-0.85]} {0.3, 1.1}},
   Graphics[{
     Inset[
      Graphics3D[{Specularity[White, 5], Black, Sphere[]}, 
       Boxed -> False, Lighting -> {{"Point", White, {0, 0, 3}}}],
      Center, Center, Scaled[0.25]],
     , {
      {EdgeForm[White], White, Disk[sph, 0.08]}, 
      Inset[Graphics3D[{Specularity[White, 5], Hue[0.05, 1, 0.8], 
         Sphere[]}, Boxed -> False, 
        Lighting -> {{"Point", Hue[0.1, 1, 1], {0, 0, 3}}, {"Ambient",
            GrayLevel[0.6]}}],
       sph, Center, Scaled[0.12]]}
     , GeometricTransformation[
      {
       {EdgeForm[White], White, Disk[sph, 0.08]},
       Inset[
        Graphics3D[{Specularity[White, 5], Hue[0.55, 0.9, 0.75],
          Sphere[]}, Boxed -> False,
         Lighting -> {{"Point", Darker[Cyan, 0.2],
        RotationTransform[2 Pi/3, {1.3, -2.4, 2}]@{0, 0, 
          3}}, {&quot;Ambient&quot;, GrayLevel[0.6]}}],
    sph, Center, Scaled[0.12]]},
  RotationTransform[-2 Pi/3]
  ]
 , GeometricTransformation[
  {
   {EdgeForm[White], White, Disk[sph, 0.08]},
   Inset[
    Graphics3D[{Specularity[White, 5], Darker[Green, 0.3], 
      Sphere[]},
     Boxed -&gt; False,
     Lighting -&gt; {{&quot;Point&quot;, Darker[Yellow, 0.3],

        RotationTransform[-2 Pi/3, {1.3, -2.4, 2}]@{0, 0, 
          3}}, {&quot;Ambient&quot;, GrayLevel[0.6]}}],
    sph, Center, Scaled[0.12]]},
  RotationTransform[2 Pi/3]
  ]
 }, PlotRange -&gt; 1, PlotRangePadding -&gt; Scaled[.05]]

];
Show[
 Graphics[Inset[paths, Center, Center, Scaled[1.8]],
  PlotRange -> 1, PlotRangePadding -> Scaled[.05]],
 spheres]

What version of Mathematica you are using? I tried this code with Mathematica 12. The orbits are well but with no sphere. — Saeid, Dec 09 '20 at 21:41
I uploaded the generated output. You see some extra white lines. Also, I see the figure you uploaded has a much better resolution. What kind of format you used? I used png and jpeg. Both did not give me high resolution. — Saeid, Dec 09 '20 at 21:59
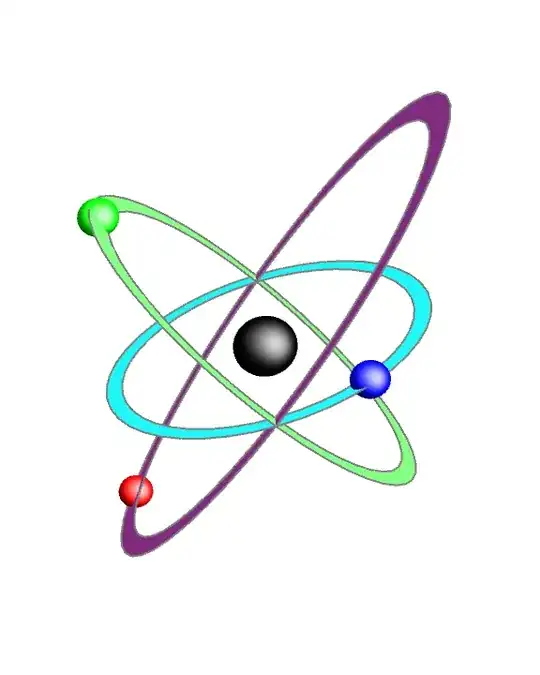
I copied the image from Mathematica and pasted it into the stackexchange edit box. — Michael E2, Dec 09 '20 at 22:10
@Saeid Try change rot to something bigger in the 3rd column: rot = { {1, 0, 1/8}, {0, 1, 1/8} }. The problem appears to be that the graphics engine is computing the paths as intersecting. I got such a figure when I had 1/100 in the 3rd column. But you don't want the numbers to get too big or you might distort the figure. Since 1/10 is big enough for me but not for you, I cannot predict how big you have to make it. Play with it. — Michael E2, Dec 09 '20 at 22:14
@Saeid I suppose you could also try different RenderingOptions. — Michael E2, Dec 09 '20 at 22:19
I played with the numbers you mentioned above and the issue is solved. Thank you so much. — Saeid, Dec 10 '20 at 00:41
@Saeid : If Exporting to JPEG, try altering ImageSize and ImageResolution. For PNG, try altering ImageSize, "CompressionLevel", Dithering, and "QuantizationMethod". — Eric Towers, Dec 10 '20 at 08:44

score 9 · Answer 2 · answered Dec 09 '20 at 09:49

One of many ways to get 3D hollow disks is to use Annulus[] to specify the region in Plot3D:

p3d = Plot3D[{x + y, x/2, -y}, {x, y} ∈ Annulus[{0, 0}, {.9, 1}], 
   Mesh -> None, MaxRecursion -> 5, PlotPoints -> 90,
   BoundaryStyle -> Directive[Thick, Gray], Lighting -> "Neutral", 
   PlotStyle -> {Lighter @ Magenta, Cyan, Lighter @ Green}];

Place the spheres at random points on the centers of the orbit annuli:

boxratios = {1, 1, 3};
SeedRandom[1]
g3d = Graphics3D[{Black, Specularity[White, 10], 
    Scale[Sphere[{0, 0, 0}, .2], 1/boxratios], 
    MapThread[{#, Scale[Sphere[Append[#2 @ #3] @ #3, .12], 1/boxratios]} &, 
     {{Red, Blue, Green}, {Total, First[#]/2 &, -Last[#] &}, 
      RandomPoint[Circle[{0, 0}, .95], 3]}]}];
Show[p3d, g3d , Boxed -> False, BoxRatios -> boxratios, Axes -> False,
 ImageSize -> Large, Lighting -> "Neutral", ViewPoint -> {5/4, -3/4, 3},
 PlotRange -> All, PlotRegion -> {{0, 1}, {-0.2, 1.3}}]

+1 and wishing I could upvote your answer more. Elegance emerging from deep knowledge of the wide range of things Mma can do. I always learn something from your answers. — Jagra, Dec 09 '20 at 14:57

David G. Stork · Answer 3 · 2020-12-09T16:24:54.087

6

A start:

Graphics3D[
 {Specularity[White, 10], 
  Black, Sphere[],
  Red, Sphere[{1, 1, 1}, .3],
  Blue, Sphere[{-1, -1, 1}, .3],
  Green, Sphere[{-1, 1, 1}, .3]},
 Lighting -> {{"Point", White, {3, 0, 5}}},
 Boxed -> False]

edited Dec 09 '20 at 16:24

answered Dec 09 '20 at 04:55

David G. Stork

41,180
3
34
96

You nailed your spheres so well, I borrowed them for my answer. – Jagra Dec 09 '20 at 14:19

Jagra · Answer 4 · 2020-12-09T06:09:01.473

Second thoughts (borrowing some code from How to draw a circle in 3d on a sphere):

circle3D[centre_ : {0, 0, 0}, radius_ : 1, normal_ : {0, 0, 1}, 
  angle_ : {0, 2 Pi}] := 
 Composition[Line, 
   Map[RotationTransform[{{0, 0, 1}, normal}, centre], #] &, 
   Map[Append[#, Last@centre] &, #] &, 
   Append[DeleteDuplicates[Most@#], Last@#] &, Level[#, {-2}] &, 
   MeshPrimitives[#, 1] &, DiscretizeRegion, If][
  First@Differences@angle >= 2 Pi, Circle[Most@centre, radius], 
  Circle[Most@centre, radius, angle]]
Graphics3D[{
  circle3D[{1, 0, 1}, 2],
  circle3D[{1, 0, 1}, 1.8],
  circle3D[{1, 0, 1}, 2, {1, -1, 1}],
  circle3D[{1, 0, 1}, 1.8, {1, -1, 1}],
  circle3D[{1, 0, 1}, 2, {1, -1, -1}],
  circle3D[{1, 0, 1}, 1.8, {1, -1, -1}],
  {Opacity[0.95], Sphere[{1, 0, 1}, .5]},
  {Blue,Specularity[White, 10], Sphere[{-0.5, -0.56, 2}, .15]},
  {Red,Specularity[White, 10], Sphere[{2.88, 0, 1.01}, .15]},
  {Green,Specularity[White, 10], Sphere[{0, 0.6, -0.6}, .15]}
  },
 Boxed -> False]

More to come, e.g.:

Better placement of the orbiting spheres (maybe animate the orbits ;-)
Fill between the concentric circles forming the disks.
Color variance/gradations of disks.
Angles of the disks.

Maybe wrap all of this in a Manipulate so one could vary this sort of stuff and get the design you want.

So basically, YES one can do this in Mathematica.

Drawing hollow disks in 3D with an sphere in center and small spheres on the rings

4 Answers4

Linked