Issue with the Laplacian in Cylindrical Coordinates

Question

I am using Mathematica 12.1.1 and am unable to get the correct result for a simple laplacian in 3D Cylindrical Coordinates. I want to reproduce the following result on Mathematica: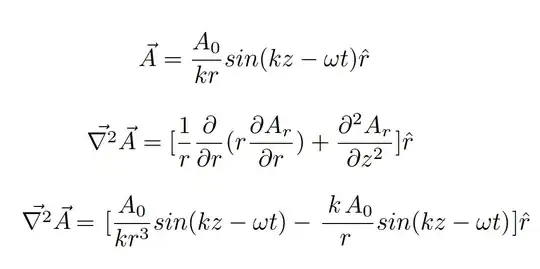

But, I am only getting the second term from the above result. Here's the code I am using:

APotential = {A0/(k r) Sin[k z - ω t], 0, 0};
Laplacian[APotential, {r, θ, z}, "Cylindrical"]
(* OUTPUT IS: {-((A0 k Sin[k z-t ω])/r),0,0} *)

Is this because of a bug, or am I missing something?

Hi, you made a typo. In the definition of the pot. the angle is called: t, but in the Laplacian the angle is called theta. — Daniel Huber, Dec 09 '20 at 20:03
Yup, as @BillWatts said, t refers to time, while θ is the azimuth angle. — Sid, Dec 10 '20 at 03:42

score 4 · Accepted Answer · answered Dec 09 '20 at 22:15

4

The Laplacian takes a scalar argument, so if you want to take the Laplacian of a vector you need to do each component separately. This works:

Ar[r_, θ_, z_] = A0/(k r) Sin[k z - ω t]
Laplacian[Ar[r, θ, z], {r, θ, z}, "Cylindrical"]
((A0 Sin[k z - t ω])/(k r^3) - (A0 k Sin[k z - t ω])/r)

answered Dec 09 '20 at 22:15

Bill Watts

8,217
1
11
28

Oh, thanks a lot! So, if Aθ and Az were non zero as well, would I have to calculate them separately and then add the final results? – Sid Dec 10 '20 at 03:40
2

To be honest, I've never seen them added together, and I'm not sure what that would be physically. Assigning the pieces to vector components would be OK if you really need them to form a vector. – Bill Watts Dec 10 '20 at 06:36
Ah alright. Thank you again – Sid Dec 10 '20 at 17:45
1

You are welcome. But I am puzzled at Mathematica's answer to your code. It seems to me that if it cannot calculate the Laplacian for a vector, it should return unevaluated, rather than return the wrong answer. – Bill Watts Dec 11 '20 at 01:20
1

@SiddharthChaini As to how Mathematica deals with Laplacian of a vector, you may want to read this: https://mathematica.stackexchange.com/q/225423/1871 – xzczd Oct 16 '22 at 03:35

score 1 · Answer 2 · answered Dec 10 '20 at 01:39

1

For general vector field {f[r, t, z], g[r, t, z], h[r, t, z]}, the Laplacian is

Laplacian[{f[r, t, z], g[r, t, z], h[r, t, z]}, {r, t, z}, 
  "Cylindrical"] // Expand

So we write

APotential = {A0/(k r) Sin[k z - ω t], 0, 0};
Laplacian[APotential, {r, t, z}, "Cylindrical"] // Expand

answered Dec 10 '20 at 01:39

cvgmt

72,231
4
75
133

1

Hi, actually the azimuth angle is θ, while t refers to time. So the basis will be {r, θ, z} and not {r, t, z}. That still gives an error. However, Bill's answer worked well instead. Thank you nevertheless. – Sid Dec 10 '20 at 03:44

Issue with the Laplacian in Cylindrical Coordinates

2 Answers2