Generate random lines that don't be too crowded between the intersections

Question

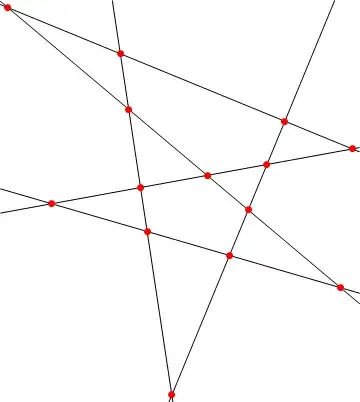
It's easy to generate random lines, such as this

n = 8;
lines = InfiniteLine /@ RandomReal[1, {n, 2, 2}];
points = RegionIntersection @@@ Subsets[lines, {2}];
Graphics[{lines, Red, points}, PlotRangePadding -> Scaled[.2]]

If there are more lines, some of the points of intersection between them will be very close

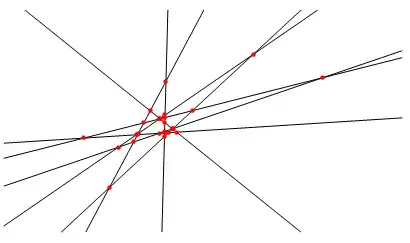
But I want to get something like this

This means making the distance between the intersections and and the angle between the lines as uniform as possible. I thought of a brute force method, very slow, is there a more efficient method?

n = 6;
(Label["begin"];
 lines = InfiniteLine /@ RandomReal[{-1, 1}, {n, 2, 2}];
 intersectionPts = First /@ RegionIntersection @@@ Subsets[lines, {2}];
 If[! AllTrue[EuclideanDistance @@@ Subsets[intersectionPts, {2}], 
    0.2 < # < n &], Goto["begin"]])
EuclideanDistance @@@ Subsets[intersectionPts, {2}] // MinMax
Graphics[{lines, Red, Point@intersectionPts}, PlotRange -> All, 
 PlotRangePadding -> Scaled[.1]]

I'll state the obvious: these won't be really random lines any more, if that really matters. I think the easiest would be to start from the intersection points actually, then build back the lines. Find yourself a method to pick intersection points distributed the way you want, then build back the lines from those? — MarcoB, Dec 15 '20 at 16:58
this may be useful for some part of the task: Efficient way to generate random points with a predefined lower bound on their pairwise Euclidean distance — kglr, Dec 15 '20 at 18:47

flinty · Answer 1 · 2020-12-18T18:31:42.903

You could try to add lines as you go, rejecting them if they create any intersections that are too close together then trying again, or adding them to the list if they meet a minimum distance criterion. This isn't always guaranteed to work as it's possible there are too many crowded lines early on, but in that case you can always change the seed until you get a good configuration.

SeedRandom[1234];
(* return the minimum distance between any intersection points *)
test[lines_] :=
 Min[EuclideanDistance @@@ 
   Subsets[GraphicsMeshFindIntersections@lines, {2}]]
(* generate a random line *)
genline[] := InfiniteLine@RandomReal[{-1, 1}, {2, 2}]
(* try to generate a new line. Accept it into the list if min test passes )
addnewline[lines_, mindistance_] := 
 Module[{newlines = lines, testline},
  Do[
   testline = genline[];
   If[Length[lines] == 
      1 || (test[Append[newlines, testline]] > mindistance),
    AppendTo[newlines, testline]; Break[]];
   , {100}]; (do nothing after max attempts *)
  Return[newlines] 
  ]
(* repeatedly add new lines to list until we have n of them. Try at most 1000 iterations *)
n = 6;
mind = 0.6;
lines = NestWhile[addnewline[#, mind] &, {genline[]}, Length[#] < n &,
    1, 1000];
(* draw the lines *)
Graphics[{
  lines,
  Red, PointSize[Large],
  Point@GraphicsMeshFindIntersections@lines
  }]

score 1 · Answer 2 · answered Dec 15 '20 at 21:31

1

We could e.g. create a grid of n x n points:

n = 10; (* grid length*)
pts = Flatten[Table[{x, y}, {x, n}, {y, n}], 1];

And then choose from this grid at random m tripplets of crossing points:

m = 5; (* # of tripplets *)
int = Table[RandomSample[pts, 3], m]

And finally draw lines through all the crossing points:

Graphics[{InfiniteLine[##[[1 ;; 2]]], InfiniteLine[##[[2 ;; 3]]], 
    InfiniteLine[##[[{1, 3}]]]} & /@ int]

answered Dec 15 '20 at 21:31

Daniel Huber

51,463
1
23
57

I don't want three lines have a common intersection. – expression Dec 16 '20 at 01:39
They do not. Look at the code. 3 points make 3 different intersections. – Daniel Huber Dec 16 '20 at 08:40
@expression Perhaps you should express it thus: The intersections of three lines taken pairwise should be a minimum distance apart. You will need to specify the distance. – Michael E2 Dec 18 '20 at 01:58

Generate random lines that don't be too crowded between the intersections

2 Answers2