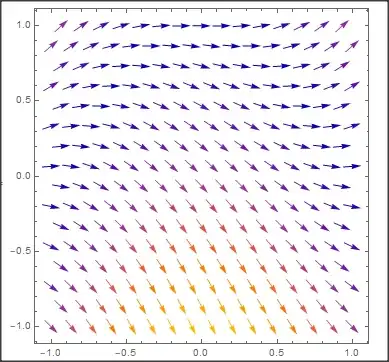
How to construct the direction field for y' = y -cos π/2 x I have tried the Plot function Plot[Derivative[1][y][x] == y[x] - (cos π x)/2, y[x], x]
Asked
Active
Viewed 153 times
0
MarcoB
- 67,153
- 18
- 91
- 189
Andres E Vicente
- 15
- 3
2 Answers
0
You can get the direction field by: {1,y'}, that is, at point {x,y} the increase in y is y'[x] if x increases by 1:
VectorPlot[{1, y - Cos[ Pi x/2]}, {x, -1, 1}, {y, -1, 1}]
Daniel Huber
- 51,463
- 1
- 23
- 57
-
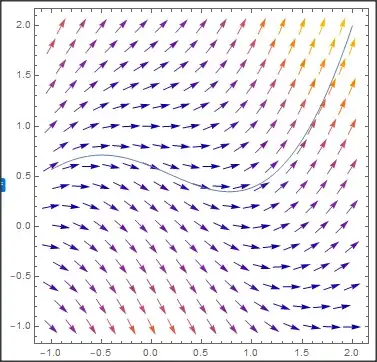
good! how to highlight the curve that satisfies y (2)= 2 on the same grid! – Andres E Vicente Dec 17 '20 at 21:04
0
eq = {y'[x] == y[x] - Cos[Pi x/2], y[2] == 2};
fun[x_] = y[x] /. DSolve[eq, y, {x, 0, 4}][[1]];
Show[{
VectorPlot[{1, y - Cos[Pi x/2]}, {x, -1, 2}, {y, -1, 2}],
Plot[fun[x], {x, -1, 2}, PlotRange -> All]
}]
Daniel Huber
- 51,463
- 1
- 23
- 57