How to construct the direction field for y' = y- cos\[Pi]/2x

Question

How to construct the direction field for y' = y -cos π/2 x I have tried the Plot function Plot[Derivative[1][y][x] == y[x] - (cos π x)/2, y[x], x]

Answer 1

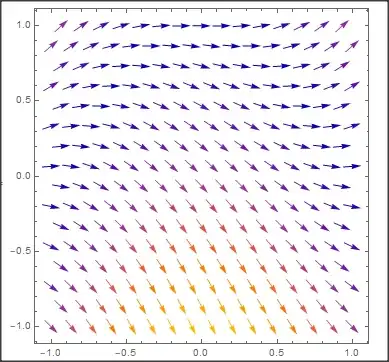
You can get the direction field by: {1,y'}, that is, at point {x,y} the increase in y is y'[x] if x increases by 1:

VectorPlot[{1, y - Cos[ Pi x/2]}, {x, -1, 1}, {y, -1, 1}]

Answer 2

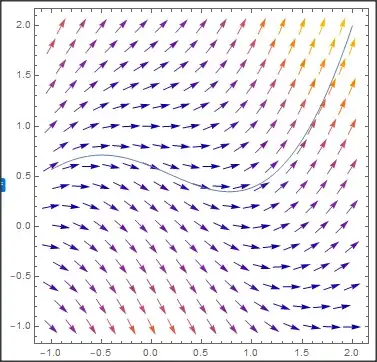
eq = {y'[x] == y[x] - Cos[Pi x/2], y[2] == 2};
fun[x_] = y[x] /. DSolve[eq, y, {x, 0, 4}][[1]];
Show[{
  VectorPlot[{1, y - Cos[Pi x/2]}, {x, -1, 2}, {y, -1, 2}],
  Plot[fun[x], {x, -1, 2}, PlotRange -> All]
  }]