I am interested in finding eigenvalues of Schrödinger-type equations, a prototype example being
$$- w^{\prime \prime } (y) - 6 \operatorname{sech}^2 (y) w(y) + w(y) = \lambda w(y)$$
I posted a question on the same equation in Solving a Sturm-Liouville problem and got great help there, both on symbolic methods as well as a numeric approach which delivers the sought result.
Out of curiosity, I have experimented also NDEigensystem and another alternative, described below, and would like to know what is that I am doing wrong with those, as I am not able to recover the same results.
Using NDEigensystem, setting Dirichlet boundary conditions at $\pm 20$ to mimick the real conditions at infinity, $w(y) \to 0$ as $ y \to \infty$ I tried
L = 20
{eigN2, funcN2} =
N @ DEigensystem[{w[y] - 6 Sech[y]^2 w[y] - w''[y],
DirichletCondition[w[y] == 0, True]}, w[y], {y, -L, L}, 12,
Method -> {"Arnoldi", "Criteria" -> "RealPart"}];
Plot[funcN2, {y, -20, 20}, PlotLegends -> eigN2]
I get a warning message
ParametricNDSolveValue::bvluc: The equations derived from the boundary
conditions are numerically ill-conditioned. The boundary conditions may
not be sufficient to uniquely define a solution. If a solution is computed,
it may match the boundary conditions poorly.
Is this a working precision issue? I found a post stating that NDEigensystem cannot work with arbitrary precision. Can the issue be circumvented by a better choice of boundary conditions or what else?
In any case, I get only positive eigenvalues (which do exist and are related to oscillatory eigenfunctions, is the boundary conditions definition not satisfactory?). I used
Method -> {"Arnoldi", "Criteria" -> "RealPart"}
as I think it should sort the eigenvalues by magnitude, as I found on another post, but I am not successful (there should be an eigenvalue equal to $-3$), as documented on my first post on the equation linked above. The equation as written here is obtained by a change of variables from the original one, as documented in the answer by bbgodfrey.
I have also tried the approach detailed in the following post Find eigen energies of time-independent Schrödinger equation. I know the eigenfunction I am interested is even, so I use the b.c. $w'(0) = 0$:
U[x_] := -6*Sech[x]^2
L = 20
pfun2 = ParametricNDSolveValue[{ -ψ''[x] +
U[x] ψ[x] + ψ[x] == Ei ψ[x], ψ'[0.] ==
0., ψ[L] == 0.}, ψ, {x, -L, L}, {Ei}]
Show[Plot[U[x], {x, -5, 5}, PlotStyle -> Directive[Thick, Green]],
Plot[Evaluate@Table[Re[pfun2[Ei][x]], {Ei, -3, 2, 1}], {x, -L, L}],
PlotRange -> {All, {-6, 10}}]
val2 = Map[FindRoot[pfun2[Ei][-L], {Ei, #}] &, {1, 2, 3}]
{{Ei -> 1.02897}, {Ei -> 2.00241}, {Ei -> 3.00088}}
and there is no negative eigenvalue, nor the related eigenfunction.
Any hint would be greatly appreciated.
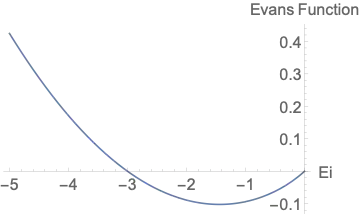
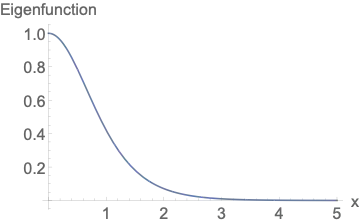
-2.90075which is not very far from-3. (Certainly this will come closer to-3if you refine the discretization.) – Henrik Schumacher Dec 23 '20 at 15:20DirichletCondition[w[y] == 0, True]atL=10. So let tryL=10and remove bc and optionMethod -> {"Arnoldi", "Criteria" -> "RealPart"}in v. 12.2 – Alex Trounev Dec 23 '20 at 15:39