Collect terms in inverse powers of three variables

Question

I have the following expression

-(((-(L/r1) + L/r2)^2*(L/r1 - L/r3)^2*(-(L/r2) + L/r3)^2)/(1 + 1/r1 + 1/r2 + 1/r3)^2) + (1 + L^2/r1 + ((-(L/r1) + L/r2)*(L/r1 - L/r3))/(1 + 1/r1 + 1/r2 + 1/r3))*
   (1 + L^2/r2 + ((-(L/r1) + L/r2)*(-(L/r2) + L/r3))/(1 + 1/r1 + 1/r2 + 1/r3))*(1 + 1/r1 + 1/r2 + 1/r3)*(1 + ((L/r1 - L/r3)*(-(L/r2) + L/r3))/(1 + 1/r1 + 1/r2 + 1/r3) + 
    L^2/r3)

Which I want to rewrite by collecting according to the inverse powers of r1, r2 and r3. That is, I want to get

1 + (1 + L^2)/r1 + (1 + L^2)/r2 + (1 + L^2)/r3 + (3*L^2 + L^4)/(r1*r2) + (3*L^2 + L^4)/(r1*r3) + (3*L^2 + L^4)/(r2*r3) + (9*L^4 + L^6)/(r1*r2*r3) - 
   L^6/(r1^2*r2^2) - L^6/(r1^2*r3^2) - L^6/(r2^2*r3^2) + (2*L^6)/(r1*r2*r3^2) + (2*L^6)/(r1*r2^2*r3) + (2*L^6)/(r1^2*r2*r3)

I have done this by hand, but for more complciated expressions I want to use Mathematica. I tried Collect[expression,{r1,r2,r3},Simplify] but it did nothing for me. Also, I do not want to collect in powers of L.

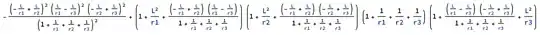
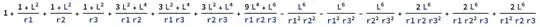
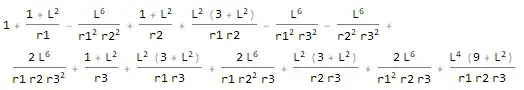
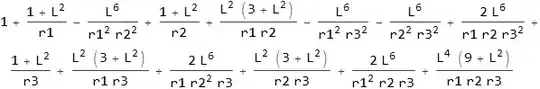
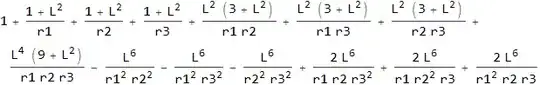
You can get the coefficients of 1/r1,1/r2,1/r3 using: CoefficientList[expression, {1/r1, 1/r2, 1/r3}] Look it up in the help, for the output format — Daniel Huber, Dec 28 '20 at 17:58

MarcoB · Answer 1 · 2020-12-28T17:57:34.210

3

Here is a pretty manual approach:

Total[
  Simplify@*Total /@
    GatherBy[
      List @@ Expand[FullSimplify@expr],
      Denominator
    ]
]

edited Dec 28 '20 at 17:57

answered Dec 28 '20 at 17:51

MarcoB

67,153
18
91
189

This is nice. Do you think it is possible to get the output in the order I have specified above? – ThunderBiggi Dec 28 '20 at 19:11
Maybe start with yours: Block[{sepTerms, invSepTerms}, sepTerms = Total[Simplify @* Total /@ GatherBy[List @@ Expand[Simplify[Together[Qf[x, y, z] /. {1/Sqrt[(x - x1)^2 + y^2 + (z - z1)^2] -> 1/r1, 1/Sqrt[(x - x2)^2 + y^2 + (z - z2)^2] -> 1/r2, 1/Sqrt[(x - x3)^2 + y^2 + (z - z3)^2] -> 1/r3}]]], Denominator]]; invSepTerms = CoefficientRules[test /. {r1 -> ir1^(-1), r2 -> ir2^(-1), r3 -> ir3^(-1)}, {ir1, ir2, ir3}]; invSepTerms = SortBy[invSepTerms, Total[#1[[1]]] & ]; Apply[Times, ({r1, r2, r3}^(-#1) & ) /@ invSepTerms[[All,1]], {1}]*invSepTerms[[All,2]]] – ThunderBiggi Dec 28 '20 at 19:43
@ThunderBiggi Plus has the attribute Orderless, which means it sorts its arguments into a canonical order. Just try to keep y + x in the order y + x. You have to use something like Hold[y + x] or Defer[y + x] to keep the terms from being sorted. – Michael E2 Dec 28 '20 at 19:59
@MichaelE2 I always struggle with all the Hold functions, as they either stay there and prevent me from doing anything, or just disappear and do nothing. Where am I supposed to use it here? – ThunderBiggi Dec 28 '20 at 20:11
2

@ThunderBiggi I don't know because it depends. I was hoping you would just learn to live with the standard Plus ordering. Here are a couple of Q&A related to fixing the order of Plus: (15744), (188576). If you need the order just for [tag:output-formatting], there is hope. If you need to do further calculation with it, it is best to let Plus do its own thing, imo. – Michael E2 Dec 28 '20 at 20:24

kglr · Accepted Answer · 2020-12-29T07:34:13.247

Total @ Factor @ MonomialList[Simplify @ expr, 1/{r1, r2, r3}]

To have the terms in a specific order, sort the monomials as you like and wrap the resulting list with Apply[Defer @* Plus]:

Apply[Defer @* Plus] @ 
  SortBy[Through @ {Total, Sort} @ Exponent[#, 1/{r1, r2, r3}] &] @
    Factor @ MonomialList[Simplify @ expr, 1/{r1, r2, r3}]

Using an alternative ordering of terms:

Apply[Defer @* Plus] @ Factor @ 
   MonomialList[Simplify @ expr, 1/{r1, r2, r3}, "NegativeDegreeReverseLexicographic"]

Collect terms in inverse powers of three variables

2 Answers2