4

This table with a caption that said "First three words you see will come to you in 2021" inspired me to do some digging:

Imagine that we have a table with randomly filled letters. How can Mathematica identify the words inside that table? I wrote these lines:

minWordLength = 3; (* Declare the minimum length of a word *)

substrings[str_String, len_:minWordLength] := With[{r = StringLength[str]},
  Join@@ Table[StringTake[str, {i, j}], {i, r+1}, {j, i+len-1, r}] ];


highlights[str_String] := With[{pos =
  Union@@ (Range@@ (Flatten[#, 1]&)@ StringPosition[str, #]&/@
  Select[substrings[str], DictionaryWordQ[#, IgnoreCase-> True]&] )},
  MapIndexed[If[MemberQ[pos, First@ #2], Style[#, Red], #]&, Characters@str] ] ;


findwords[table_] := With[{list = If[StringQ@table,
  StringPartition[ToUpperCase@table, Sqrt@StringLength@table],
  ToUpperCase/@ table]},
  Grid[highlights/@ list, Frame-> All] ];

As you see, the argument of findwords can either be a string containing all the letters inside the table, or a list of strings that contain the letters in each row. This code highlights the words found in the dictionary with red color. For example, if we write:

str = StringJoin@ RandomChoice[CharacterRange["a", "z"], 256];
findwords[str]

then the result will be something like this:

output of the code

Now there are several issues with this code that I cannot figure out how to solve. I'll appreciate any help.

  1. Sometimes there are a few seemingly gibberish words highlighted in the table. Some of them appear to be abbreviations. For example, as you see in the above picture, LLL or XXV or LII are not actual words. I wasn't able to get rid of these, because DictionaryWordQ doesn't have any options to specify which kind of words we are seeking. Is there any way to filter those?
  2. This code can only find horizontal words. Can we modify it to find vertical words as well? (Maybe highlighted with another color). I struggled a bit with the idea of transposing the table and then doing the same process on transposed table. But the process became way too complicated and furthermore, I wasn't able to highlight the resulting vertical words alongside the horizontal ones. Is there some kind of a neat trick to do this?
  3. And as a bonus point, what about diagonal words? For this one I had no clue, not even a tiny one.
polfosol
  • 952
  • 5
  • 20
  • "what about diagonal words" - have you tried using Diagonal[]? – J. M.'s missing motivation Jan 02 '21 at 18:50
  • @J.M. yes I have. But then again, finding the indices and then highlighting them became a real headache. – polfosol Jan 02 '21 at 18:51
  • Not identical but overlapping (5387). – Pillsy Jan 02 '21 at 19:15
  • @C.E. in that question, we know what words we are looking for. Here we don't – polfosol Jan 03 '21 at 03:50
  • You can take a list of all English words I suppose, if you want it to be general. The solutions can also be modified to use CommonWordQ as in Anton’s answer. – C. E. Jan 03 '21 at 08:26
  • @C.E. an do you think that would be efficient? If I didn't get you wrong, you are basically talking about a brute-force search of all the English words inside a table, one by one. – polfosol Jan 03 '21 at 08:34
  • I guess that’s basically what CommonWordQ does. Anyway, the point is that the word search part is solved in that question already. Columns, rows, diagonals, reversed words, all that is implemented there. If it can be shown that performance is a problem then it would make a great new question to take one of the solutions and ask how it can be made more efficient for all of the English language. But as it stands this question has a very big overlap with that other question, enough that I would call it a duplicate question. – C. E. Jan 03 '21 at 09:41
  • @C.E. NO CommonWordQ does not do that – polfosol Jan 03 '21 at 10:08
  • 2
    This question is closed as a duplicate of "Solving word search puzzles" because of question's somewhat misleading title. I do not see finding the words as the primary (or only) challenge in the question. I think the requests for quality and display of the results are not answered in "Solving word search puzzles" . – Anton Antonov Jan 03 '21 at 14:38

1 Answers1

6

Updated answer

As a follow up question, can we apply a different strategy for distinguishing the words? For example, adding a frame instead of coloring them.

Answering the follow up question does bring better looking and easier to read results:

aResFr =
  findwords[str, CommonWordQ,
   <|Horizontal -> (Framed[Style[#, Blue, Bold], 
        Background -> Yellow] &),
    Vertical -> (Framed[Style[#, Red], Background -> LightBlue] &),
    Diagonal -> (Framed[Style[#, Purple, Bold], 
        Background -> GrayLevel[0.9]] &)|>];
Grid[#, Dividers -> All] & /@ aResFr

enter image description here

Grid[CombineHighlights[aResFr], Dividers -> All]

enter image description here

The update definitions below are based on the definitions of the first answer with some relatively small code refactoring. The function signatures have to be "relaxed" to take "highlighter function" as an argument.

Definitions

(*Declare the minimum length of a word*)
minWordLength = 3;

ClearAll[substrings];
substrings[str_String, len_ : minWordLength] :=


Block[{r = StringLength[str]},
   Join @@ Table[StringTake[str, {i, j}], {i, r + 1}, {j, i + len - 1, r}]
   ];


ClearAll[wordsFinder];
wordsFinder[str_String, dictWordFunc_ : DictionaryWordQ, 
   highlighterFunc_ : (Style[#, Red] &)] :=
  Block[{pos, res},
   pos = Union @@ (Range @@ (Flatten[#, 1] &)@StringPosition[str, #] & /@ 
       Select[substrings[str], dictWordFunc[#, IgnoreCase -> True] &]);
   MapIndexed[If[MemberQ[pos, First@#2], highlighterFunc[#], #] &, 
    Characters@str]
   ];


ClearAll[highlightsDiag];
highlightsDiag[str_String, dictWordFunc_ : DictionaryWordQ, 
   highlighterFunc_ : (Style[#, Red] &)] :=


Block[{matChars, n, matInds, res},
   matChars = Partition[Characters@str, Sqrt[StringLength[str]]];
   n = Length[matChars];
   matInds = Table[{i, j}, {i, n}, {j, n}];
   res = Table[
     AssociationThread[Diagonal[matInds, i], 
      wordsFinder[StringJoin @@ Diagonal[matChars, i], dictWordFunc, 
       highlighterFunc]], {i, -n + 1, n - 1}];
   Normal[SparseArray[Normal[Join @@ res]]]
   ];


ClearAll[highlights];
highlights[str_String, dir_, dictWordFunc_ : DictionaryWordQ, 
   highlighterFunc_ : (Style[#, Red] &)] :=


Block[{matChars, n, matInds, res},
    matChars = Partition[Characters@str, Sqrt[StringLength[str]]];
    If[TrueQ[dir === Vertical],
     matChars = Transpose[matChars]
     ];
    n = Length[matChars];
    matInds = Table[{i, j}, {i, n}, {j, n}];
    res = Table[
      AssociationThread[matInds[[i]], 
       wordsFinder[StringJoin @@ matChars[[i]], dictWordFunc, 
        highlighterFunc]], {i, n}];
    res = Normal[SparseArray[Normal[Join @@ res]]];
    If[TrueQ[dir === Vertical],
     Transpose[res],
     (ELSE)
     res
     ]
    ] /; MemberQ[{Vertical, Horizontal}, dir];


ClearAll[findwords];
findwords[table_, dictWordFunc_ : DictionaryWordQ, 
   highlighterFunc_ : (Style[#, Red] &), opts : OptionsPattern[]] :=


Block[{str},
    str = If[MatrixQ[table], StringJoin @@ Flatten[table], table];
    str = ToUpperCase[str];
    <|


 &quot;Horizontal&quot; -&gt; 
  highlights[str, Horizontal, dictWordFunc, 
   If[AssociationQ[highlighterFunc], highlighterFunc[Horizontal], 
    highlighterFunc]],
 &quot;Vertical&quot; -&gt; 
  highlights[str, Vertical, dictWordFunc, 
   If[AssociationQ[highlighterFunc], highlighterFunc[Vertical], 
    highlighterFunc]],
 &quot;Diagonal&quot; -&gt; 
  highlightsDiag[str, dictWordFunc, 
   If[AssociationQ[highlighterFunc], highlighterFunc[Diagonal], 
    highlighterFunc]]
 |&gt;
] /; (SquareMatrixQ[table] || StringQ[table]);




Clear[CombineHighlights];
CombineHighlights[aTbls_Association] :=


Map[If[VectorQ[#, StringQ], First[#], Last@Select[#, Not@*StringQ]] &, 
   Transpose[Values[aTbls], {3, 1, 2}], {2}];


Clear[CommonWordQ];
aCommonWords = 
  AssociationThread[ToLowerCase@Union[RandomWord["CommonWords", 10^6]], 
   True];
CommonWordQ[w_String, opts : OptionsPattern[]] := 
  Lookup[aCommonWords, ToLowerCase@w, False];

First answer

Here are brief descriptions of my way of answering OP's questions:

  1. We can define CommonWordQ function based on RandomWord["CommonWords"].

  2. One way to do it is to refactor OP's code:

    • Rename OP's highlights into wordsFinder.

    • Create functions for horizontal and vertical words highlights making them utilize rules for SparseArray.

  3. Diagonal words highlights are similar to the horizontal and vertical words highlights finding, but using Diagonal instead of Part.

Note, that:

  • I tried to reuse OP's code, as much as possible.

  • I combine the tables into one, but the results are hard to read.

  • Further refactoring can put other Style element, not just color.

  • The refactored functions take as arguments: string, is-it-a-word function, and color (or an association of colors).

Definitions

(*Declare the minimum length of a word*)
minWordLength = 3;

ClearAll[substrings];
substrings[str_String, len_ : minWordLength] :=

  Block[{r = StringLength[str]},
   Join @@ 
    Table[StringTake[str, {i, j}], {i, r + 1}, {j, i + len - 1, r}]
   ];


ClearAll[wordsFinder];
wordsFinder[str_String, dictWordFunc_ : DictionaryWordQ, color_ : Red] :=
  Block[{pos, res},
    pos = 
     Union @@ (Range @@ (Flatten[#, 1] &)@StringPosition[str, #] & /@ 
        Select[substrings[str], 
         dictWordFunc[#, IgnoreCase -> True] &]);
    MapIndexed[If[MemberQ[pos, First@#2], Style[#, color], #] &, 
     Characters@str]
    ] /; ColorQ[color];


ClearAll[highlightsDiag];
highlightsDiag[str_String, dictWordFunc_ : DictionaryWordQ, color_ : Red] :=
  Block[{matChars, n, matInds, res},
    matChars = Partition[Characters@str, Sqrt[StringLength[str]]];
    n = Length[matChars];
    matInds = Table[{i, j}, {i, n}, {j, n}];
    res = 
     Table[AssociationThread[Diagonal[matInds, i], 
       wordsFinder[StringJoin @@ Diagonal[matChars, i], dictWordFunc, 
        color]], {i, -n + 1, n - 1}];
    Normal[SparseArray[Normal[Join @@ res]]]
    ] /; ColorQ[color];


ClearAll[highlights];
highlights[str_String, dir_, dictWordFunc_ : DictionaryWordQ, color_ : Red] :=
  Block[{matChars, n, matInds, res},
    matChars = Partition[Characters@str, Sqrt[StringLength[str]]];
    If[TrueQ[dir === Vertical],
     matChars = Transpose[matChars]
     ];
    n = Length[matChars];
    matInds = Table[{i, j}, {i, n}, {j, n}];
    res = 
     Table[AssociationThread[matInds[[i]], 
       wordsFinder[StringJoin @@ matChars[[i]], dictWordFunc, 
        color]], {i, n}];
    res = Normal[SparseArray[Normal[Join @@ res]]];
    If[TrueQ[dir === Vertical],
     Transpose[res],
     (ELSE)
     res
     ]
    ] /; MemberQ[{Vertical, Horizontal}, dir] && ColorQ[color];


ClearAll[findwords];
findwords[table_, dictWordFunc_ : DictionaryWordQ, color_ : Red, opts : OptionsPattern[]] :=
  Block[{str},
    str = If[MatrixQ[table], StringJoin @@ Flatten[table], table];
    str = ToUpperCase[str];
    <|


 &quot;Horizontal&quot; -&gt; 
  highlights[str, Horizontal, dictWordFunc, 
   If[ColorQ[color], color, color[1]]],
 &quot;Vertical&quot; -&gt; 
  highlights[str, Vertical, dictWordFunc, 
   If[ColorQ[color], color, color[2]]],
 &quot;Diagonals&quot; -&gt; 
  highlightsDiag[str, dictWordFunc, 
   If[ColorQ[color], color, color[3]]]
 |&gt;
] /; (SquareMatrixQ[table] || StringQ[table]);




Clear[CombineHighlights];
CombineHighlights[aTbls_Association] :=


Map[If[VectorQ[#, StringQ], First[#], 
     Last@Select[#, Head[#] === Style &]] &, 
   Transpose[Values[aTbls], {3, 1, 2}], {2}];


Clear[CommonWordQ];
aCommonWords = AssociationThread[ToLowerCase@Union[RandomWord["CommonWords", 10^6]], True];
CommonWordQ[w_String, opts : OptionsPattern[]] := Lookup[aCommonWords, ToLowerCase@w, False];

Tables for dictionary words

str = StringJoin@RandomChoice[CharacterRange["a", "z"], 256];

Grid[#, Dividers -> All] & /@ findwords[str, DictionaryWordQ, Red]

enter image description here

Tables for common words

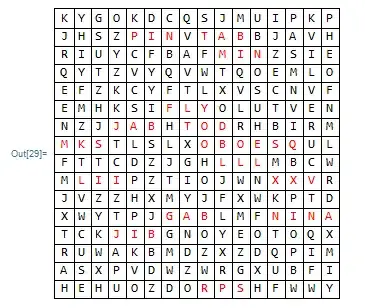
Grid[#, Dividers -> All] & /@ findwords[str, CommonWordQ, Red]

enter image description here

Combining the tables

Combining the tables does not look that good (in my opinion):

aRes3 = findwords[str, CommonWordQ, <|1 -> Red, 2 -> Blue, 3 -> Green|>];
Grid[CombineHighlights[aRes3], Dividers -> All]

enter image description here

Anton Antonov
  • 37,787
  • 3
  • 100
  • 178
  • Thanks. This is inarguably perfect already. As a follow up question, can we apply a different strategy for distinguishing the words? For example, adding a frame instead of coloring them. – polfosol Jan 03 '21 at 04:57
  • @polfosol Yes, but some refactoring has to be done. (Some of the function signatures have to be "relaxed" to take highlighter function as an argument.) See my update. – Anton Antonov Jan 03 '21 at 14:22