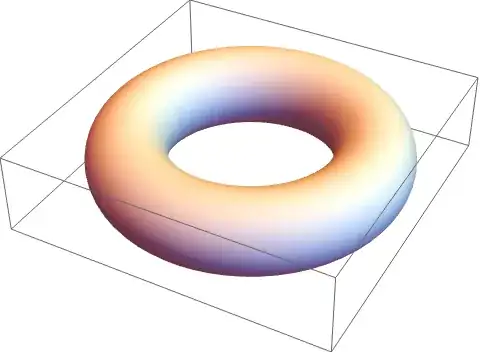
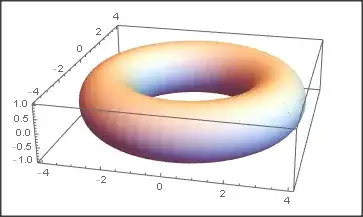
Using the Tube function to create a torus from an equation for the curve

Question

I've been searching for an answer for this for a while now, but I can't find anything that deals with using the Tube function to generate a torus from the equation of the torus.

The equation of my torus is z^2==1 - (Sqrt[x^2 + y^2] - 3 I want to use Tube and Graphics3D to show this torus. I would have thought that

Tube[z^2==1 - (Sqrt[x^2 + y^2] - 3, 1]

the second argument being the radius of the tube, would suffice, but I when I evaluate this in Graphics3D:

 Graphics3D[Tube[z^2 == 1 - (Sqrt[x^2 + y^2] - 3)^2, 1]]

I get the following error:

Coordinate False should be a triple of numbers, or a Scaled form.

Why? What am I doing incorrectly here? Thanks!

score 6 · Answer 1 · answered Jan 03 '21 at 17:11

Graphics3D[
 Tube[
  BSplineCurve[
   {{-3/2, 0, 1/2}, {-3/2, -3/2, 1/2}, {0, -3/2, 1/2},
    {3/2, -3/2, 1/2}, {3/2, 0, 1/2}, {3/2, 3/2, 1/2},
    {0, 3/2, 1/2}, {-3/2, 3/2, 1/2}, {-3/2, 0, 1/2}},
   SplineDegree -> 2, 
   SplineWeights -> {1, 1/Sqrt[2], 1, 1/Sqrt[2], 1, 1/Sqrt[2], 1,  1/Sqrt[2], 1}, 
   SplineKnots -> {0, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 4}], 
  1/2]
 ]

Adapted from an example in the docs for Tube:

PieChart3D[{1}, ChartElementFunction -> "TorusSector3D", 
 SectorOrigin -> {Automatic, 1}, BoxRatios -> Automatic]

For those interested, there is a BSplineSurface-based torus on site in this answer by @J.M.. — Michael E2, Jan 04 '21 at 00:20

score 5 · Accepted Answer · edited Jan 04 '21 at 04:35

5

Here is the torus using Graphics3D and Tube:

Graphics3D[Tube[Table[3 {Cos[p], Sin[p], 0}, {p, 0, 2 Pi, Pi/30}], 1],
  Axes -> True]

edited Jan 04 '21 at 04:35

J. M.'s missing motivation

124,525
11
401
574

answered Jan 03 '21 at 15:04

Daniel Huber

51,463
1
23
57

1

Ah, the need to parametrise was what I was missing. Many thanks! – TubularHell Jan 03 '21 at 15:18

score 3 · Answer 3 · answered Jan 03 '21 at 16:05

3

You can also use Tube as a styling directive with ParametricPlot3D:

ParametricPlot3D[3 {Cos[p], Sin[p], 0}, {p, 0, 2 Pi}, 
 PlotStyle -> Tube[1], PlotRangePadding -> Scaled[.15]]

answered Jan 03 '21 at 16:05

kglr

394,356
18
477
896

score 2 · Answer 4 · answered Jan 03 '21 at 14:38

2

ImplicitRegion[
  z^2 == 1 - (Sqrt[x^2 + y^2] - 3)^2, {x, y, z}] // Region

ContourPlot3D[
 z^2 == 1 - (Sqrt[x^2 + y^2] - 3)^2, {x, -4, 4}, {y, -4, 4}, {z, -4, 
  4}, Boxed -> False, Axes -> False]

answered Jan 03 '21 at 14:38

cvgmt

72,231
4
75
133

1

Thank you! This is a much easier way to do it. My question relates to an exercise in my Mathematica course whereby I have to use Graphics3D and Tube in conjunction to achieve the required shape. Any ideas on this? Thanks – TubularHell Jan 03 '21 at 14:50

Using the Tube function to create a torus from an equation for the curve

4 Answers4