Montgomery Modular Exponentiation

Question

I'm trying to write a Montgomery exponentiation based on this which can compete with Mathematica PowerMod. We know that PowerMod uses square and multiply technique. The speedup must be obtained by replacing modular operation mod n with modular operation mod 2^x. Can we accomplish this in Mathematica such that it take over from PowerMod? This is my implementation:

Global variables:

RLength = 0; R = 0; RM1=0; RInverse = 0; NPrime = 0; verbose = False;

and the MontExp (b^e mod n):

MontExp[b_, e_, n_] := (RLength = BitLength[n]; R = 2^RLength; RM1=R-1; 
  RInverse = PowerMod[R, -1, n]; NPrime = PowerMod[-n, -1, R]; 
  M = Mod[b*R, n]; Result = Mod[R, n]; 
  If[verbose, 
   Print["MontParams: R=", R, ", RInverse=", RInverse, " ,NPrime=", 
    NPrime, " ,M=", M]];
  Do[Result = Mont[Result, Result, n]; 
   If[expBit == 1, Result = Mont[Result, M, n]], {expBit, 
    IntegerDigits[e, 2]}]; Result = Mont[Result, 1, n]; Return[Result])

Mont function version 0:

Mont[u_, v_, n_] := (z = Mod[u*v*RInverse, n]; 
  If[verbose, Print["Monto ", u, " * ", v, " => ", z]]; Return[z]); 

Mont function version 1:

Mont[u_, v_, n_] := (t = u*v; 
   z = BitShiftRight[(t + Mod[t*NPrime, R] n), RLength]; 
   If[verbose, Print["Monto ", u, " * ", v, " => ", z]]; Return[z]);

Mont function version 2:

Mont[u_, v_, n_] := (t = u*v; 
   z = BitShiftRight[(t + BitAnd[t*NPrime, RM1] n), RLength]; 
   If[verbose, Print["Monto ", u, " * ", v, " => ", z]]; Return[z]);

and Timings:

p = 2^20000 + 1;

Mathematica PowerMod:

Timing[PowerMod[2, p, p] == 2]

{1.529, False}

Mont v0

{3.432, False}

Mont v1

{7.332, False}

Mont v2

{3.541, False}

As you can see as I tried to improve it with binary shifts instead of modular operations, it had negative impact on the speed. That's probably because of non-native implementation in Mathematica. Any idea to improve it?

--

Update

I've learnt that Mod[b, 2^n] == BitAnd[b, 2^n-1] so I changed the Version 2 to use BitAnd, but yet no gain in compare to original PowerMod...

Update 2

It seems that because of its reliance on shifts, the speedups are only for 2^k+1 numbers. However I saw an amazing result from @Simoon-Woods answer:

list = (2^# + 1) & /@ Range[5000, 100000, 5000];

PowerModTimings = First[Timing[PowerMod[2, #, #]]] & /@ list
    {0.047,0.265,0.717,1.529,2.871,4.336,6.506,9.173,11.934,16.879,20.623,25.772,30.373,37.3,45.49,55.131,63.274,73.788,85.114,96.112}

MontExpTimingsV2 = First[Timing[MontExp[2, #, #]]] & /@ list (*Mont version 2*)
    {0.063,0.156,0.312,0.483,5.258,0.92,4.711,1.56,8.081,18.642,2.949,3.51,16.13,18.268,36.91,5.569,15.413,28.236,106.143,60.388}

MontExpTimingsV0 = First[Timing[MontExp[2, #, #]]] & /@ list (*Mont version 0*)
{0.047,0.093,0.188,0.234,2.418,0.53,2.246,0.858,3.417,8.58,1.451,1.669,7.051,8.003,18.221,2.824,6.91,13.245,51.231,29.047}

And plotting the result:

ListLinePlot[{PowerModTimings, MontExpTimingsV2, MontExpTimingsV0}]

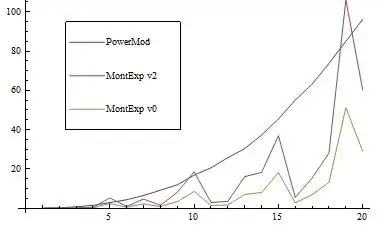
Update 3

I've added timings for Mont version 0 based on @Simon-Woods answer. Great timings ...

Answer 1

For the example problem I get about a factor of 4 speedup over PowerMod by memoizing Mont. This of course means that Mont should not contain any global variables so I rewrote the code slightly:

MontExp[b_, e_, n_] := Module[
  {RLength, R, RM1, RInverse, NPrime, M, Result},
  RLength = BitLength[n]; R = 2^RLength; RM1 = R - 1;
  RInverse = PowerMod[R, -1, n]; NPrime = PowerMod[-n, -1, R];
  M = Mod[b R, n]; Result = Mod[R, n];
  Do[
   Result = Mont[Result, Result, n, NPrime, RM1, RLength];
   If[expBit == 1, Result = Mont[Result, M, n, NPrime, RM1, RLength]]
   , {expBit, IntegerDigits[e, 2]}];
  Mont[Result, 1, n, NPrime, RM1, RLength]];

mem : Mont[u_, v_, n_, NPrime_, RM1_, RLength_] :=
 mem = Module[{t = u v}, BitShiftRight[(t + BitAnd[t*NPrime, RM1] n), RLength]]

Testing:

p = 2^20000 + 1;

Timing[res1 = PowerMod[2, p, p];]
(* {3.546, Null} *)

Timing[res2 = MontExp[2, p, p];]
(* {0.765, Null} *)

res1 == res2
(* True *)