Accuracy of Mod[x, 1] and FractionalPart[x]

Question

The difference between exact and numerical computation is clear to me. But why is

{7.2 - 7 == 8.2 - 8, 
8.2 - 8 == 9.2 - 9,
(7.2 - 7) - (8.2 - 8) > 0, 
(8.2 - 8) - (9.2 - 9) == 0}

equal to

{True, True, True, True}

(same behavior with Mod[n + 0.2, 1]and FractionalPart[n + 0.2])

and why has (n + 0.2) - n $12$ different values when the integer $n$ runs from $0$ to $10^6$? Indeed

Tally[Table[(n + .2) - n, {n, 0, 10^6}]] // Length

gives 12. Only (n + 0.) - n and (n + 0.5) - n always give the same answer.

Answer 1

Two insightful responses were left in comments which I think are worth summarizing here as answers:

• As J.M. mentioned, Equal has a tolerance within which the two arguments are considered equal. This is controlled by Internal`$EqualTolerance (see e.g. this question, among others).

• Regarding the second question, Michael mentioned that the machine real representation of a decimal input is the nearest fraction of the form $a/2^p$, where $a$ is an integer with $1≤a<2^{53}$ (as long as the decimal number is not too big or too small in absolute value). When a number like 0.2 that is not of the form b / 2^q (with q relatively small, such as 1/2 == 0.5 or 3/8 == 0.375) — when it is added from n, the round-off error changes with n somewhat. Note (n + 0.375) - n gives the same answer too up to around 5 * 10^15. Try Table[(n + 0.5) - n, {n, 1*10^15, 1*10^16, 10^15}] to see a change in round-off.

Answer 2

From the help of Equal:

"Approximate numbers with machine precision or higher are considered equal if they differ in at most their last seven binary digits (roughly their last two decimal digits)."

Note, that "their last 2 decimal digits" must be interpreted by taking into account. that ending zeros are not written and that machine numbers have approx. 16 decimal digits.

Now considering the first 4 questions that give True. If we write LHS and RHS separately:

{{7.2 - 7, 8.2 - 8}, {8.2 - 8, 
   9.2 - 9}, {(7.2 - 7), (8.2 - 8)}, {(8.2 - 8), (9.2 - 
     9)}} // FullForm

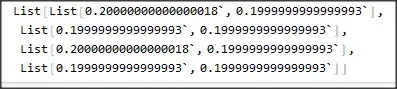
We see, that they differ at most by the 2 last decimal digits and are therefore considered equal.

On the other hand, the question with Tally: From the help of Tally:

"Tally[list] is equivalent to Tally[list,SameQ]."

And from the help of SameQ:

"SameQ requires exact correspondence between expressions, except that it still considers Real numbers equal if they differ in their last binary digit."

SameQ is therefore more stringent than Equal. Additionally, remember that this corresponds to approx. 16 decimal digits with machine numbers. If we write both terms to be subtracted separately:

Tally[Table[{(n + 0.2) - n}, {n, 0, 10^6}]][[All, 1]] // FullForm

We get:

And we see that these values differ more than the 16.th decimal digits.