Plot intersection (elliptic curve) of two quadrics

Question

Consider a $3d$ system with variables $x,\,y,\,z$ and two surfaces defined by the functions

$\qquad f(x,y)=0$ and $g(x,y,z)=0$.

I am interested in the intersection of these two surfaces giving an elliptic curve. That is, I would like to plot $f(x,y)=0$ under the condition that $0=g(x,y,z)$ (or equivalently the other way around). I've tried with ContourPlot3d the following

ContourPlot3D[
  {f(x, y) == 0, 0 == g(x, y, z)}, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, 
  AxesLabel -> {"x", "y", "z"},   
  Contours -> {0}, 
  ContourStyle -> Opacity[0.0], 
  Mesh -> None,
  BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Thick, Green}}}, 
  PerformanceGoal -> "Quality"]

However, I wonder if there is a better way and also if one could go around the BoundaryStyle-option by some '&&' enforcing the simultaneous plotting/solution of both equations.

All remarks are welcome!

Edit

After a remark the second equation was correctly written down.*

The functions are given as

$\qquad f(x,y)=4 x y - \left(\frac{660}{4x+4y-45}+15-2x\right)^2=0$

and

$\qquad g(x,y,z)=\left(\frac{660}{2x +z-15}+45- 4x -4y\right)=0$.

It would also be great to know, how to extract the algebraic form of the curve, perhaps also in parameterized form.

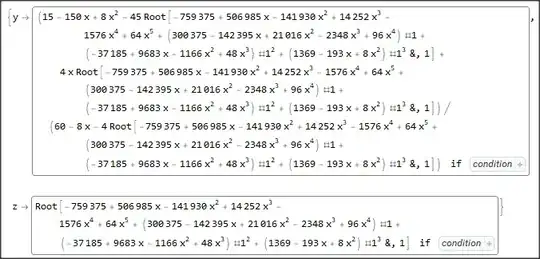
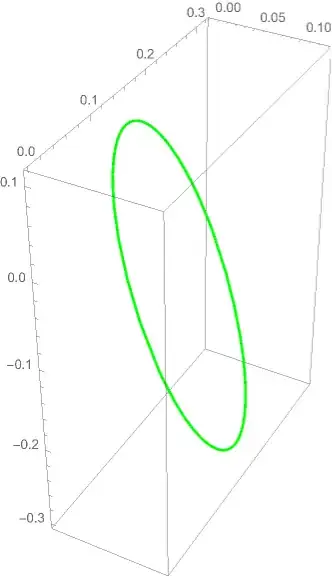
Surely you can't have used {f(x,y)==0,z==g(x,y)} exactly, since that is not correct Mathematica syntax. So what was your expression, and the definitions of f and g? — MarcoB, Jan 08 '21 at 22:02
If the answers to the linked question do not suit your needs,then edit your question to explain why. — J. M.'s missing motivation, Jan 08 '21 at 22:26
Thanks, the question was edited. @J. M., I've edited the question. Apart from plotting a nice result it would be great to know how to extract the algebraic form of the curve itself. — Hamurabi, Jan 08 '21 at 22:38
I am not certain what you are expecting as the algebraic form, since the two algebraic equations taken together already (implicitly) represent your curve. If it's a parametrization, that can be nontrivial, but one of the answers in the linked question talks about how to use an ODE formulation to numerically compute one. — J. M.'s missing motivation, Jan 08 '21 at 22:40

score 2 · Answer 1 · answered Jan 09 '21 at 10:11

2

You may get the intersections parametrized by e.g. x:

res = Solve[{f[x, y] == 0, g[x, y, z] == 0}, {y, z},Reals];

This gives 3 lengthy solutions. E.g. the first one:

containing conditions that read e.g.:

answered Jan 09 '21 at 10:11

Daniel Huber

51,463
1
23
57

score 2 · Answer 2 · answered Jan 09 '21 at 13:19

Found Daniel's solution interesting and wanted to extend it just a bit to plot the result. Only the first 2 solutions I found were needed. Notice I had to draw two plots and hard-code the limit 0<x<0.12949. Might be a challenge to extract the limits directly and express the solution as a single, perhaps conditional function, for a single parameter say

$$h(t)=\{t,y(t),z(t)\}; \quad 0<=t<=1$$

Ran into problems doing this though so left as is.

f[x_, y_] := 4 x y - (660/(4 x + 4 y - 45) + 15 - 2 x)^2;
g[x_, y_, z_] := (660/(2 x + z - 15) + 45 - 4 x - 4 y);
theSols = NSolve[{f[x, y] == 0, g[x, y, z] == 0}, {y, z}, Reals];
myFun1[x_, y_, z_] = Flatten[{x, {y, z} /. theSols[[1]]}];
pp1 = ParametricPlot3D[myFun1[x, y, z], {x, 0, 0.12949}, 
   PlotStyle -> Blue];
myFun2[x_, y_, z_] = Flatten[{x, ({y, z} /. theSols[[2]])}];
pp2 = ParametricPlot3D[myFun2[x, y, z], {x, 0, 0.12949}, 
   PlotStyle -> Red];
Show[{pp1, pp2}, BoxRatios -> {1, 1, 1}, AxesLabel -> {"x", "y", "z"}]

cvgmt · Answer 3 · 2021-01-09T15:27:09.693

Edit

Region work in this simple situation.

f[x_, y_] = 4 x*y - (660/(4 x + 4 y - 45) + 15 - 2 x)^2;
g[x_, y_, z_] = 660/(2 x + z - 15) + 45 - 4 x - 4 y;
Region[ImplicitRegion[{f[x, y] == 0 , 
   g[x, y, z] == 0}, {{x, -1, 1}, {y, -1, 1}, {z, -1, 1}}], 
 Axes -> True, Boxed -> True, BaseStyle -> {Thick, Green}]

Original

BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Thick, Green}}} to find intersection of two surfaces is too slow.

Here we just draw one of the implicit surface and add Mesh according to the second condition.

f[x_, y_] = 4 x*y - (660/(4 x + 4 y - 45) + 15 - 2 x)^2;
g[x_, y_, z_] = 660/(2 x + z - 15) + 45 - 4 x - 4 y;
ContourPlot3D[{g[x, y, z] == 0}, {x, -1, 1}, {y, -1, 1}, {z, -1, 
  1}, AxesLabel -> {"x", "y", "z"}, Mesh -> {{0}}, 
 MeshFunctions -> Function[{x, y, z}, f[x, y]], 
 MeshStyle -> {Thick, Green}, ContourStyle -> Opacity[0.02], 
 BoundaryStyle -> None]

Or

f[x_, y_] = 4 x*y - (660/(4 x + 4 y - 45) + 15 - 2 x)^2;
g[x_, y_, z_] = 660/(2 x + z - 15) + 45 - 4 x - 4 y;
ContourPlot3D[{f[x, y] == 0}, {x, -1, 1}, {y, -1, 1}, {z, -1, 
  1}, AxesLabel -> {"x", "y", "z"}, Mesh -> {{0}}, 
 MeshFunctions -> Function[{x, y, z}, g[x, y, z]], MeshStyle -> {Thick, Green}, ContourStyle -> Opacity[0.02], BoundaryStyle -> None]

Plot intersection (elliptic curve) of two quadrics

Edit

3 Answers3