I'm looking for an efficient way to construct a sinc interpolation i.e. an interpolating function of a list of numbers in the form of a Fourier series with a chosen maximum frequency. The input list is supposed to be an equidistant sample of some real smooth function (e.g. a function with a finite-support Fourier transform) and the interpolation should be a continuous function that is a sum of harmonic functions (cosine and sine functions) such that their coefficients are equal to the Fourier coefficients of the list for all frequencies up to the chosen max frequency, (see Wikipedia: Whittaker–Shannon interpolation formula). Increasing the max frequency beyond the band-limit of the original function should give a perfect reconstruction of it. I'd guess there is a predefined Mathematica function doing that but I couldn't find it.
One way would be to apply Interpolation on the list, then NFourierSeries on the resulting InterpolationFunction (choosing the desired max frequency), but this is obviously very inefficient. LowpassFilter should be doing something similar but the output is a list, not a function. One option for an efficient solution that I'm trying to implement is to compute the Fourier coefficients from the list using Fourier, construct a function that is a list of harmonic functions with the right frequencies (e.g. Table[Sin[2 Pi n #/T], {n, nmax}] & for sines) and then Dot-multiply the two lists. I found this excellent post that computes the correct factors: Numerical Fourier transform of a complicated function

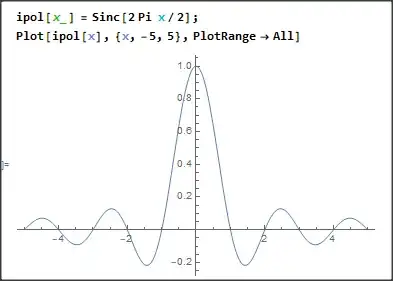

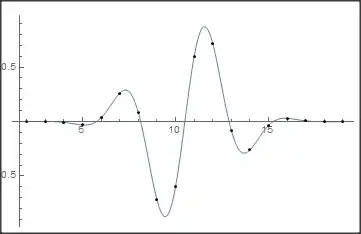

Sumwhich is slow for large lists. – spyros Jan 10 '21 at 12:06NFourierSeries, you should find that all the additional terms are zero. An efficient way of doing sinc-interpolation is to Fourier transform, zero-pad the spectrum, then inverse Fourier transform. – mikado Jan 10 '21 at 13:03Compile. – spyros Jan 10 '21 at 19:27