2

Excuse me can you help me on solving the following differential equation by Mathematica ?!

$$d^2y[x]/dx^2-(1/(x+a))*dy[x]/dx+(m*x+L)y[x]=0$$

i had try on it as following :

ode=D[y[x],{x,2}]-1/(x+a)*D[y[x],x]+(m*x+L)*y[x]==0
DSolve[ode,y[x],x]

it gives me strange output :

{{y[x] -> DifferentialRoot[Function[{\[FormalY], \[FormalX]}, 
      {(\[FormalX] + a)*(L + \[FormalX]*m)*\[FormalY][\[FormalX]] - 
         Derivative[1][\[FormalY]][\[FormalX]] + 
         (\[FormalX] + a)*Derivative[2][\[FormalY]][
           \[FormalX]] == 0, \[FormalY][0] == C[1], 
       Derivative[1][\[FormalY]][0] == C[2]}]][x]}}
Michael E2
  • 235,386
  • 17
  • 334
  • 747
Aya
  • 69
  • 4

1 Answers1

5
Clear["Global`*"]

Use a numeric technique.

First, include some arbitrary initial conditions.

ode = {D[y[x], {x, 2}] - 1/(x + a)*D[y[x], x] + (m*x + L)*y[x] == 0, 
   y[0] == y0, y'[0] == yp0};

sol = ParametricNDSolve[ode, y, {x, -5, 5}, {m, a, L, y0, yp0}];


Manipulate[
 Plot[y[m, a, L, y0, yp0][x] /. sol, {x, -5, 5}],
 {{m, 1}, -5, 5, 0.1, Appearance -> "Labeled"},
 {{a, 1}, -5, 5, 0.1, Appearance -> "Labeled"},
 {{L, 1}, -5, 5, 0.1, Appearance -> "Labeled"},
 {{y0, 0}, -5, 5, 0.1, Appearance -> "Labeled"},
 {{yp0, 1}, -5, 5, 0.1, Appearance -> "Labeled"}]

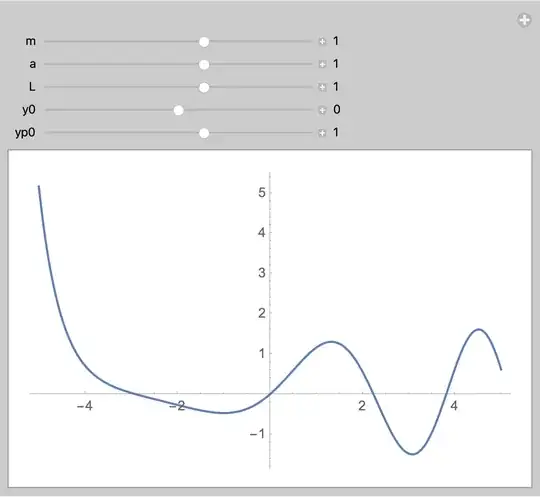
enter image description here

An analytic solution may be available for specific values of the parameters. For example,

ode2 = ode /. {m -> 1, a -> 1, L -> 1, y0 -> 0, yp0 -> 1}

(* {(1 + x) y[x] - Derivative[1][y][x]/(1 + x) + (y^[Prime][Prime])[x] == 0, 
 y[0] == 0, Derivative[1][y][0] == 1} *)


sol2 = DSolve[ode2, y, x][[1]]


(* {y -> Function[{x}, -(((-1)^(
        1/3) (AiryAiPrime[(-1)^(1/3) + (-1)^(1/3) x] AiryBiPrime[(-1)^(1/3)] -
           AiryAiPrime[(-1)^(
            1/3)] AiryBiPrime[(-1)^(
             1/3) + (-1)^(1/3) x]))/(-AiryAiPrime[(-1)^(1/3)] AiryBi[(-1)^(
          1/3)] + AiryAi[(-1)^(1/3)] AiryBiPrime[(-1)^(1/3)]))]} *)

Verifying the solution

ode2 /. sol2 // Simplify

(* {True, True, True} *)


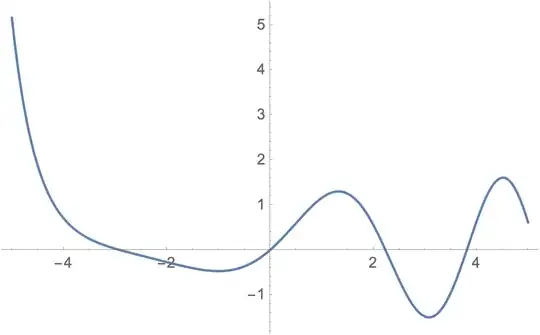
Plot[y[x] /. sol2, {x, -5, 5},
 PlotPoints -> 50, MaxRecursion -> 5,
 WorkingPrecision -> 20]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Many thanks , but you mean that this differential equation does not have solution except when m=1,L=1,a=1<y0=0 and yp0=1 ??? – Aya Jan 10 '21 at 19:11
  • No, I said that analytic solutions may be available and that {m -> 1, a -> 1, L -> 1, y0 -> 0, yp0 -> 1} is an example. There may be other cases with an analytic solution. There are numerous case with a numeric solution as shown in the Manipulate. – Bob Hanlon Jan 10 '21 at 19:51
  • yes i saw this , but i need a general solution ,, How can i get it please ? – Aya Jan 10 '21 at 20:03
  • 2
    If Mathematica gives you a DifferentialRoot solution, it means it couldn't find anything better and that a general analytic solution in all likelihood doesn't exist. – Sjoerd Smit Jan 10 '21 at 20:07