4

I have an integral equation for a value t between the limits of integration 1 and a parameter u. I am trying to solve for u with known values of t ranging from 0 to 14 in steps of 1

I am not sure how to go about this calculation, any help would be appreciated!

My code is:

eq = 1/(ξ (-1.66334 - 0.44 Log[ξ] + 1.66116 ξ))
t = NIntegrate[eq, {ξ, 1, u}]

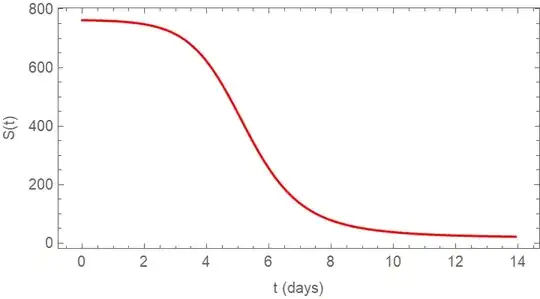
Essentially this is being used for the following plot:

S = 762*u
p1 = 
  ParametricPlot[{t, S}, {u, 1, 0.02902}, 
    Frame -> True, 
    Axes -> False, 
    FrameLabel -> {"t (days)", "S(t)"}, 
    PlotRange -> All, 
    AspectRatio -> 1/2, 
    LabelStyle -> Directive[FontFamily -> "Helvetica"], 
    PlotStyle -> Red]

I am trying to find the exact values of S at various values of t. For example, I know that when t = 0, S = 762. I wish to extract data at values of t in the sequence 0, 1, ..., 14. Therefore, I thought by knowing values of u, I could work out S.

Is there an easier way to extract exact data values from a plot? I have tried using the get-coordinates` tool, but find this is not give the accuracy I require.

Plot produced is below:

enter image description here

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
scrumpy.j
  • 43
  • 4

2 Answers2

7

Alternatively, you can rephrase the problem as a differential equation and use NDSolve:

eq[x_] := 1/(x (-1.66334 - 0.44 Log[x] + 1.66116 x));
sol = First@NDSolve[{u'[t] == 1/eq[u[t]], u[0] == 1}, u, {t, 0, 14}];
uVals = Table[u[t] /. sol, {t, 0, 14}]
NIntegrate[eq[x], {x, 1, #}] & /@ uVals

{1., 0.995745, 0.981588, 0.936796, 0.814854, 0.583019, 0.334263, 0.177939, 
 0.102363, 0.0669098, 0.0492174, 0.0396957, 0.0342333,0.0309452, 0.0288969}

{0., 1.00001, 2.00001, 3.00001, 4.00001, 5.00001, 6.00001, 7.00001, 
 8.00001, 9.00001, 10., 11., 12., 13., 14.}

The integrand has poles at

Solve[1/eq[x] == 0, x]

{{x -> 0.0250815}, {x -> 1.00178}}

as well as x == 0, but these are exactly avoided by the solutions in uVals.

Hausdorff
  • 3,505
  • 1
  • 9
  • 25
3

NIntegrate can't deal with an undecided limit. So you can't directly use u here.

I tried Plot, but it looks messy.

Plot[NIntegrate[eq, {ξ, 1, x}], {x, 1, 5}]

enter image description here

Edited:

Plot[NIntegrate[eq, {ξ, 1, x}], {x, 0.1, 1}]

enter image description here

Anyway, you may want this:

expr[u_?NumericQ] := NIntegrate[ξ^2 + ξ, {ξ, 1, u}];
FindRoot[expr[u] == 1, {u, 1}] // Quiet

Which will return you a numeric solution. (I change the expression to get a solution)

From the new information, I get this:

FindRoot[NIntegrate[eq, {ξ, 1, u}] == 6, {u, 0.2}]

{u -> 0.334265}

AsukaMinato
  • 9,758
  • 1
  • 14
  • 40