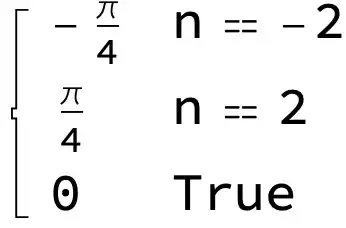A result like this appears as one of the terms when I compute coefficients in a Fourier Series:
expr =(Sin[n*Pi])/((-4 + n^2))
If I simplify all my terms, this happens:
Simplify[expr, Assumptions -> Element[n, Integers]] (*returns a zero*)
Which is true except if n=-2 or 2:
Limit[expr, n -> 2] (*give Pi/4*)
Shouldn't Simplify catching that?