ContourPlot3D, grid of cylinders

Question

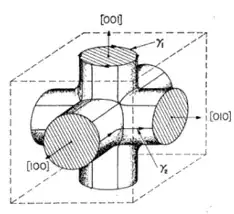
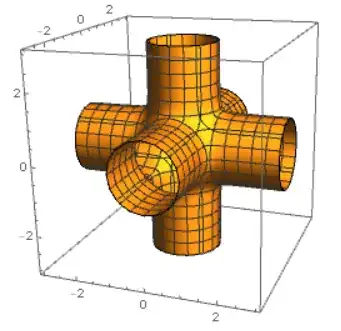
I am trying to make a 3D contour plot that looks like a grid of cylinders to represent the Fermi surface of a metal, like below:

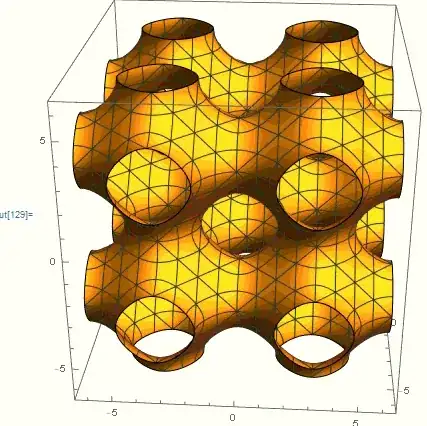
I have no problem generating something that kind of looks like it.

(Cos[x] + Cos[y] + Cos[z] == 0). (This shows multiple unit cells.)

I need it to be more cylindrical, though. I need to also later plot cross-sections of this for planes at different heights, so it is more than just wanting the accurate figure.

I think this is tricky because it is not well-suited to either cylindrical coordinates or spherical coordinates. I was thinking that I could just create three cylinders at right angles to each other and superimpose them, but I can't figure out a way to make the equation for cylinders.

Any help on this would be great!

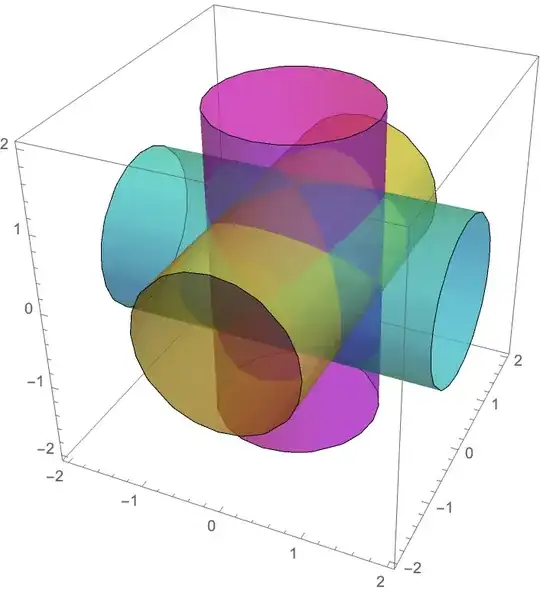
Do you want real cylinders or "smoothed cylinders" like the approaches with Cos? Should the interior be hollow or filled? — A.Z., Jan 27 '21 at 09:49
The "real cylinders" approach would correspond to Michael's and my answer, while cvgmt's answer uses a nodal surface approximation. — J. M.'s missing motivation, Jan 27 '21 at 16:44
Another approach would be to use Cylinder and RegionUnion to construct a single Region object — b3m2a1, Jan 27 '21 at 17:49
@J.M. I think that the nodal surface approximation is actually closer to the physical situation that I am modeling (Fermi surface), but your answer is also very useful. I can't seem, however, to make the cross-sections without there being little gaps in the circles using your approach (I think because of the Round[] function). — Nick, Jan 27 '21 at 18:26
@Nick, are you using the current version in my answer? Indeed, the previous formulation of my answer had those artifacts, but I do not believe the current one does. — J. M.'s missing motivation, Jan 27 '21 at 18:35

score 21 · Answer 1 · edited Jan 27 '21 at 03:36

21

Maybe add some perturbed term such as Cos[x]*Cos[y]*Cos[z] or Cos[x]*Cos[y]+Cos[y]*Cos[z]+Cos[z]*Cos[x] to Cos[x] + Cos[y] + Cos[z].

ContourPlot3D[
 Cos[x] + Cos[y] + Cos[z] - 1.5 Cos[x] Cos[y] Cos[z] == 1.5, {x, -9, 
  9}, {y, -9, 9}, {z, -9, 9}, ContourStyle -> FaceForm[Orange, Cyan], 
 Mesh -> None, Boxed -> False, Axes -> False]

edited Jan 27 '21 at 03:36

J. M.'s missing motivation

124,525
11
401
574

answered Jan 27 '21 at 02:33

cvgmt

72,231
4
75
133

This is exactly what I was thinking! – Nick Jan 27 '21 at 03:17

J. M.'s missing motivation · Answer 2 · 2021-01-28T01:59:43.937

cvgmt had the right idea to use a periodic function. Using a technique similar to what I did here, here is how to use Round[] (for periodicity) with Max[] (as a stand-in for Boolean OR):

With[{c = 1, r = 1/4}, 
     ContourPlot3D[Max[r^2 - (x - Round[x, c])^2 - (y - Round[y, c])^2, 
                       r^2 - (y - Round[y, c])^2 - (z - Round[z, c])^2, 
                       r^2 - (z - Round[z, c])^2 - (x - Round[x, c])^2] == 0,
                   {x, -3/2, 3/2}, {y, -3/2, 3/2}, {z, -3/2, 3/2}]]

cylinders

You'd need to be prepared to crank up PlotPoints and MaxRecursion for this approach (with the concomitant increase in memory requirements).

A variation of this theme is to replace Max[] with a smooth version like $\log$-sum-$\exp$:

With[{c = 1, r = 1/4, k = 30},
     ContourPlot3D[Log[Total[
                   Exp[k {r^2 - (x - Round[x, c])^2 - (y - Round[y, c])^2, 
                          r^2 - (y - Round[y, c])^2 - (z - Round[z, c])^2, 
                          r^2 - (z - Round[z, c])^2 - (x - Round[x, c])^2}]]]/k == 0,
                   {x, -3/2, 3/2}, {y, -3/2, 3/2}, {z, -3/2, 3/2}]]

smoothmax connection of cylinders

score 8 · Answer 3 · answered Jan 27 '21 at 21:43

This can perhaps be generalized easiliy to other constraints. The equation of a cylinder in the z-direction can be written as a function that evaluates to zero. \begin{align} x^2+y^2&=r^2\\ f_Z(x,y,z)=x^2+y^2-r^2&=0 \end{align} So to get an intersection of three cylinders you just multiply three of these functions together:

range = 3;
r = 1;
ContourPlot3D[
   (x^2 + y^2 - r^2) (z^2 + y^2 - r^2) (z^2 + x^2 - r^2) == 0,
      {x, -range, range}, {y, -range, range}, {z, -range, range}   
]

The nice thing is you can easily smooth this out by taking a contour slightly above zero.

ContourPlot3D[
   (x^2 + y^2 - r^2) (z^2 + y^2 - r^2) (z^2 + x^2 - r^2) == 0.05,
      {x, -range, range}, {y, -range, range}, {z, -range, range}   
]

You can make this periodic by replacing x -> Sin[x] (same for $y,z$) or by replacing x -> Mod[x, period, - period/2]. Sin[x] seems to work faster but you won't get perfect cylinders.

range = 5;
r = .5;
ContourPlot3D[(Sin[x]^2 + Sin[y]^2 - r^2) (Sin[z]^2 + Sin[y]^2 - 
     r^2) (Sin[x]^2 + Sin[z]^2 - r^2) == .005, {x, -range, 
  range}, {y, -range, range}, {z, -range, range}]

In my answer, I originally used multiplication (AND) instead of Max[] (OR), but the resulting surface had blemishes for some reason, which is why I switched to the current formulation. — J. M.'s missing motivation, Jan 28 '21 at 01:40

score 6 · Answer 4 · edited Jan 27 '21 at 04:06

6

Another way, if you want cylinders:

ddd = Min@Table[
    RegionDistance[
      InfiniteLine[{Insert[{a, b}, 0, j], Insert[{a, b}, 1, j]}]]
      [{x, y, z}],
    {a, -1, 1}, {b, -1, 1}, {j, 3}
    ];
ContourPlot3D[ddd == 1/4 // Evaluate,
 {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

edited Jan 27 '21 at 04:06

cvgmt

72,231
4
75
133

answered Jan 27 '21 at 03:35

Michael E2

235,386
17
334
747

score 5 · Answer 5 · answered Jan 26 '21 at 23:49

Maybe this is helpful

ContourPlot3D[{
  (x - 2)^2 + (y - 2)^2 == 1,
  (x + 2)^2 + (y - 2)^2 == 1,
  (x - 2)^2 + (y + 2)^2 == 1,
  (x + 2)^2 + (y + 2)^2 == 1,
(x - 2)^2 + (z - 2)^2 == 1,
  (x + 2)^2 + (z - 2)^2 == 1,
  (x - 2)^2 + (z + 2)^2 == 1,
  (x + 2)^2 + (z + 2)^2 == 1,
(y - 2)^2 + (z - 2)^2 == 1,
  (y + 2)^2 + (z - 2)^2 == 1,
  (y - 2)^2 + (z + 2)^2 == 1,
  (y + 2)^2 + (z + 2)^2 == 1
  }, {x, -5, 5}, {y, -5, 5}, {z, -5, 5}
 ]

There are probably cleverer ways to create the cylinders, depending on what you want to do with them.

If this does not need to be a contour plot, have a look at the Cylinder[] function.

Is there a way to make the grid of cylinders into a single object? When I take cross-sections it treats them all as separate, but I need it to act like a unit. — Nick, Jan 27 '21 at 01:41

b3m2a1 · Answer 6 · 2021-01-27T18:04:34.030

Just to show how to do this without ContourPlot3D and instead with Region objects

RegionUnion[
 Sequence @@ Table[
   RegionUnion[
     Cylinder[{{-1, 0, n}, {1, 0, n}}, .2],
     Cylinder[{{0, -1, n}, {0, 1, n}}, .2]
     ] // Region,
   {n, -1, 1}
   ],
 Cylinder[{{0, 0, -2}, {0, 0, 2}}, .2]
 ]

Or if you just want the boundary

tubeboundary = RegionUnion[
 Sequence @@ Table[
   RegionUnion[
     RegionBoundary@Cylinder[{{-1, 0, n}, {1, 0, n}}, .2],
     RegionBoundary@Cylinder[{{0, -1, n}, {0, 1, n}}, .2]
     ] // Region,
   {n, -1, 1}
   ],
 RegionBoundary@Cylinder[{{0, 0, -2}, {0, 0, 2}}, .2]
 ]

and this allows you to get a function for the surface

tubeboundary // RegionMember
RegionMemberFunction[
 BooleanRegion[#1 || #2 || #3 || #4 || #5 || #6 || #7 & , {RegionBoundary[
    Cylinder[{{-1, 0, -1}, {1, 0, -1}}, 0.2]], 
   RegionBoundary[Cylinder[{{0, -1, -1}, {0, 1, -1}}, 0.2]], 
   RegionBoundary[Cylinder[{{-1, 0, 0}, {1, 0, 0}}, 0.2]], << 2 >>, 
   RegionBoundary[Cylinder[{{<< 3 >>}, {<< 3 >>}}, 0.2]], 
   RegionBoundary[Cylinder[{{0, 0, -2}, {0, 0, 2}}, 0.2]]}], <>]

thorimur · Answer 7 · 2021-01-27T00:08:09.850

So, one thing you can do here is note that the equation for a cylinder extending along the z-axis is $x^2+y^2=0$, or $x^2+y^2\leq0$ for a solid cylinder. That is, it's the equation for a circle that ignores one of the axes! The other two just choose different axes to ignore. As such

RegionPlot3D[{x^2 + y^2 <= 1, y^2 + z^2 <= 1, z^2 + x^2 <= 1}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

gets you the three cylinders:

You can change the colors and styling with the options of RegionPlot3D:

RegionPlot3D[{x^2 + y^2 <= 1, y^2 + z^2 <= 1, z^2 + x^2 <= 1}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
             PlotStyle -> {Directive[Magenta, Opacity[0.5]], Directive[Cyan, Opacity[0.5]], Directive[Yellow, Opacity[0.5]]}, 
             Mesh -> False]

Importantly, you can get cross sections by And-ing (&&) these conditions with the condition for being below a plane. Consider the plane specified by $x+y-2z=0$; we have

RegionPlot3D[{x^2 + y^2 <= 1 && x + y + z/2 >= 0, 
              y^2 + z^2 <= 1 && x + y + z/2 >= 0, 
              z^2 + x^2 <= 1 && x + y + z/2 >= 0}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
             PlotStyle -> {Directive[Magenta, Opacity[0.5]], Directive[Cyan, Opacity[0.5]], Directive[Yellow, Opacity[0.5]]}, 
             Mesh -> False,
             PlotPoints -> 100]

Note that we also had to set PlotPoints to a higher number to get something that looks nice! You could make it even higher to make it look better.

(Now, you might be wondering: how do I automate this to produce a grid? And is the Cylinder graphics primitive better? Maybe. I'll try to update this answer when I have a chance later!)

score 1 · Answer 8 · answered Aug 14 '23 at 14:30

1

And yet another parameterization:

fun = E^-(x^2 + y^2)^2 + E^-(y^2 + z^2)^2 + E^-(x^2 + z^2)^2;
n = 4;
ContourPlot3D[fun == 0.1, {x, -n, n}, {y, -n, n}, {z, -n, n}, 
 PlotLabel -> TraditionalForm @ fun]

answered Aug 14 '23 at 14:30

eldo

67,911
5
60
168

Basically the log-sum-exp approach, yes. – J. M.'s missing motivation Aug 15 '23 at 21:34

ContourPlot3D, grid of cylinders

8 Answers8