Simplifying expressions after expanding

Question

I am totally new to Mathematica, so if this is a simple googleable question, I am sorry

I have this expression: $\left(e^{i \text{p1} x}-e^{-i \text{p1} x}\right) \left(e^{i \text{p2} x}-e^{-i \text{p2} x}\right) \left(e^{i \text{p3} x}-e^{-i \text{p3} x}\right) \left(e^{i \text{p4} x}-e^{-i \text{p4} x}\right) $

 (Exp[I*p1 *x] - Exp[-I*p1 *x]) (Exp[I*p2 *x] - Exp[-I*p2 *x]) (Exp[I*p3 *x] - Exp[-I*p3 *x]) (Exp[I*p4 *x] - Exp[-I*p4 *x])

I want to see it as a sum of $e^{iax}$ terms. Expand does that, but it gives: which could be further simplified as you can see by looking at it. How do I change these terms with minus signs(for eg, $p1-p2+p3-p4$) in the exponential and hence shorter?

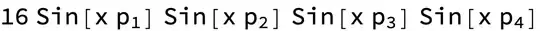
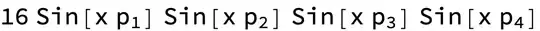
Take a look at What's the correct method to simplify exponentials? — Artes, Jan 28 '21 at 17:16
With Expand you get $e^{-i p_1 x-i p_2 x-i p_3 x-i p_4 x}-e^{i p_1 x-i p_2 x-i p_3 x-i p_4 x}-\cdots-e^{-i p_1 x+i p_2 x+i p_3 x+i p_4 x}+e^{i p_1 x+i p_2 x+i p_3 x+i p_4 x}$. With FullSimplify you get $16 \sin \left(p_1 x\right) \sin \left(p_2 x\right) \sin \left(p_3 x\right) \sin \left(p_4 x\right)$. — SnzFor16Min, Jan 28 '21 at 17:19

Bob Hanlon · Accepted Answer · 2021-01-28T18:14:43.353

1

Clear["Global`*"]

Format[p[n_]] := Subscript[p, n]

expr[n_Integer?Positive] := 
 Product[Exp[I*p[k]*x] - Exp[-I*p[k]*x], {k, 1, n}] 

expr[4] // FullSimplify

expr[4] // ComplexExpand

(expr[4] // Expand) /. E^x_ :> E^(Simplify[x])

Or,

% === Map[Simplify, expr[4] // Expand, {2}]
(* True *)

edited Jan 28 '21 at 18:14

answered Jan 28 '21 at 18:06

Bob Hanlon

157,611
7
77
198

Thanks! I was looking for the last part of your answer. – annoying_noob Jan 28 '21 at 18:37

Simplifying expressions after expanding

1 Answers1