Let us define the Legendre–Fenchel transformation of a function $f(s)$ as: $$g(j)=\max_s (js - f(s))\; .$$ I have a list of data $\{ \{s_1 , f(s_1)\} , \{ s_2, f(s_2) \},\cdots \}$. I am looking for a way to do the transformation. Any idea?
Asked
Active
Viewed 169 times
2
1 Answers
4
Here is an extension of the Legendre-Fenchel transform from data to the interpolation of data. An important hypothesis in what follows is that the function data is (strictly) convex. The derivative must be strictly increasing or the Interpolation will be faulty. The main advantage is the ability to compute the derivative of the LF transform easily.
solIF = NDSolveValue[{f''[s] == f[s] + Sin[4 f[s]], f[0] == 1,
f'[0] == 1}, f, {s, -2, 1}];
(* the function data *)
fcoords = First@solIF@"Coordinates";
fvals = solIF@"ValuesOnGrid";
data = Transpose[{fcoords, fvals}];
(* construction of the Legendre-Fenchel transform *)
lfcoords = solIF'@"ValuesOnGrid";
lfvals = fcoords*lfcoords - fvals;
lfIF = Interpolation[
Transpose@{ArrayReshape[lfcoords, {Length@lfcoords, 1}],
lfvals, fcoords}];
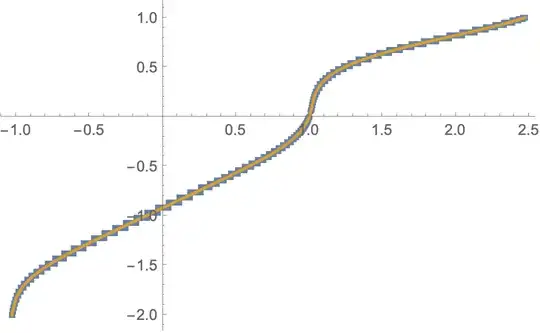
The function plot (and data in red):
ListLinePlot[solIF, Mesh -> All, MeshStyle -> Red]
The LF transform, comparing both J.M.'s Max[..] method and the interpolating function:
Plot[{Max[data . {j, -1}], lfIF[j]},
{j, First@lfcoords, Last@lfcoords},
PlotStyle -> {AbsoluteThickness[4], AbsoluteThickness[2]}]
The derivative (plotting the derivative of Max[..] takes ~13 sec. for me):
Plot[{D[Max[data . {j, -1}], j], lfIF'[j]} // Evaluate,
{j, First@lfcoords, Last@lfcoords},
PlotStyle -> {AbsoluteThickness[4], AbsoluteThickness[2]}]
Michael E2
- 235,386
- 17
- 334
- 747
-
This can be considered as the best answer to my question. Thanks a lot. – Ferhat Jan 31 '21 at 18:22
-
Could you please tell me how do I find out that solIF@"Coordinates" returns the coordinates? In other words how do I get the properties attached to something like solIF? What are the existing keywords? Thanks! – chris Jan 31 '21 at 18:29
-
3@chris I first learned about it here. You can also find the properties/methods from
solIF@"Methods". (Several high-level data structures may be queried this way or throughsolIF@"Properties".) There is a package [InterpolatingFunctionAnatomy`](https://reference.wolfram.com/language/tutorial/NDSolvePackages.html) that provides interfaces to some of the methods. – Michael E2 Jan 31 '21 at 18:48 -
-
Thanks a lot for the information. I knew about Properties but not Methods – chris Jan 31 '21 at 19:18


Max[data.{j, -1}], wheredatais your list of pairs. – J. M.'s missing motivation Jan 31 '21 at 12:28f(s_i)/s_ithen it is straightforward to figure out, for givenj, which of these is furthest. – Daniel Lichtblau Jan 31 '21 at 16:00data = Table[{s, Exp[s]}, {s, -1., 1., 1./16}]or use a nonconvex function if that is what you are interested in. (Site tip: The SE reply operator @ should not have spaces in the name, even if they are displayed. Thus: @DanielLichtblau.) – Michael E2 Jan 31 '21 at 17:19