I found DelaunayMesh works fine for 2D. For example,
coordinateList = Tuples[{Range[3], Range[3]}];
DelaunayMesh[coordinateList, PlotTheme -> "Lines"]
gives
Oddly enough, it does not work for simple regular point array like below
coordinateList = Tuples[{Range[3], Range[3], Range[3]}];
DelaunayMesh[coordinateList, PlotTheme -> "Lines"]
which just prints out the original data like
DelaunayMesh[{{1, 1, 1}, {1, 1, 2}, {1, 1, 3}, {1, 2, 1}, {1, 2,
2}, {1, 2, 3}, {1, 3, 1}, {1, 3, 2}, {1, 3, 3}, {2, 1, 1}, {2, 1,
2}, {2, 1, 3}, {2, 2, 1}, {2, 2, 2}, {2, 2, 3}, {2, 3, 1}, {2, 3,
2}, {2, 3, 3}, {3, 1, 1}, {3, 1, 2}, {3, 1, 3}, {3, 2, 1}, {3, 2,
2}, {3, 2, 3}, {3, 3, 1}, {3, 3, 2}, {3, 3, 3}},
PlotTheme -> "Lines"]
I have to jiggle each point a little to make DelaunayMesh work. Define
ClearAll[jiggleCoordinateList];
jiggleCoordinateList[coordinateList_, eta_] := Module[{},
RandomReal[eta*{-1, 1}, Dimensions@coordinateList] + coordinateList
]
then
coordinateList = Tuples[{Range[3], Range[3], Range[3]}];
DelaunayMesh[jiggleCoordinateList[coordinateList, 0.00001],
PlotTheme -> "Lines"]
gives
But why is that? I can not think of a reason why a regular point array in 3D can not be DelaunayMeshed.
Though a jiggled mesh is fine for display, for calculations, a jiggled mesh is not the same as the original mesh and will introduce error (even though it is small, it is not perfect).
Is there any workaround other than jiggling coordinates?


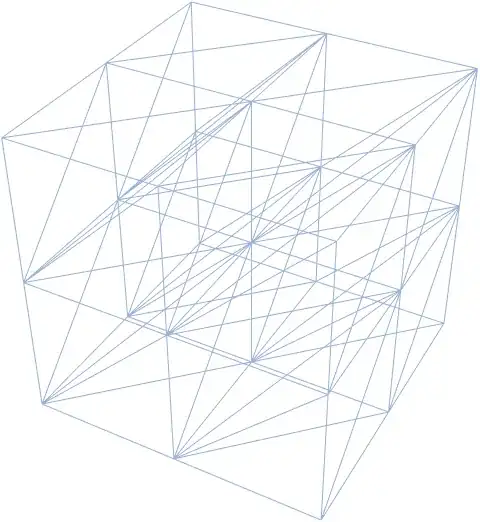
DelaunayMesh[Tuples[ConstantArray[Range[3], 3]]]seems to work fine in 11.3 ... – J. M.'s missing motivation Feb 03 '21 at 12:30