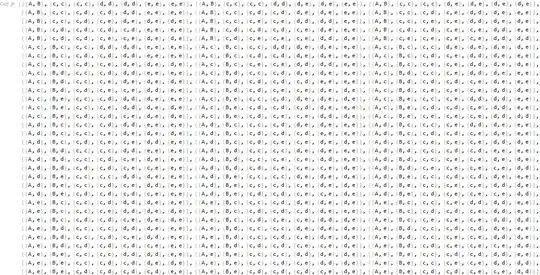How to use function `GeneratingFunction ` to solve this combinatorial problem efficiently?

Question

Divide the 14 elements {A, B, C, C, C, C, D, D, D, D, E, E, E, E} into 7 groups (one group all have two elements), and I want to find out how many kinds of methods there are without repetition.

(Sort /@ Map[
    Sort@# &, (Partition[#, 2] & /@ 
      Permutations[{A, B, c, c, c, c, d, d, d, d, e, e, e, 
        e}]), {2}]) // DeleteDuplicates

The above code is very slow, I want to know how to use generating function to solve this problem?

GeneratingFunction 
CycleIndexPolynomial
1*1*(1 + x + x^2/2 + x^3/3! + x^4/4!) (1 + x + x^2/2 + x^3/3! + x^4/
    4!) (1 + x + x^2/2 + x^3/3! + x^4/4!) // ExpandAll

score 4 · Answer 1 · answered Feb 09 '21 at 22:31

This is not an answer to your modified request for a method that uses GeneratingFunction but does address the title question about making the process more efficient.

Using your working code and because A only occurs once there are many permutations that need to be generated but then tossed. And because the resulting 96 combinations must start with either {A,B}, {A,c}, {A,d}, or {A,e}, one can make your code more computationally efficient (although maybe not humanly more efficient as it takes time to write down the efficient code):

AB = Join[{{A, B}}, #] & /@ (Sort /@ Map[Sort@# &, (Partition[#, 2] & /@ 
  Permutations[{c, c, c, c, d, d, d, d, e, e, e, e}]), {2}]) // DeleteDuplicates;
Ac = Join[{{A, c}}, #] & /@ (Sort /@ Map[Sort@# &, (Partition[#, 2] & /@ 
  Permutations[{B, c, c, c, d, d, d, d, e, e, e, e}]), {2}]) // DeleteDuplicates;
Ad = Join[{{A, d}}, #] & /@ (Sort /@ Map[Sort@# &, (Partition[#, 2] & /@ 
  Permutations[{B, c, c, c, c, d, d, d, e, e, e, e}]), {2}]) // DeleteDuplicates;
Ae = Join[{{A, e}}, #] & /@ (Sort /@ Map[Sort@# &, (Partition[#, 2] & /@ 
  Permutations[{B, c, c, c, c, d, d, d, d, e, e, e}]), {2}]) // DeleteDuplicates;
results = Join[AB, Ac, Ad, Ae]

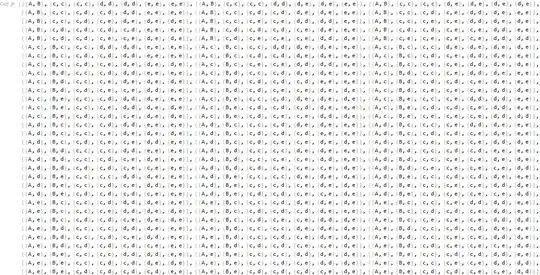
This takes around 4 seconds of computation time as opposed to around 80 seconds for the original code.

Thank you for your answer. I provide a mathematical method below. If you can, you can explain and refine it. — A little mouse on the pampas, Feb 10 '21 at 01:40

score 3 · Answer 2 · answered Feb 09 '21 at 17:10

3

You could try the following code that produces elements each with 7 groups of ```{A, B, C, C, C, C, D, D, D, D, E, E, E, E}``

data = {"A", "B", "C", "C", "C", "C", "D", "D", "D", "D", "E", "E", 
   "E", "E"};
IntegerPartitions[Length[data], {7}];
Permutations /@ %;
Join @@ %;
Internal`PartitionRagged[data, #] & /@ %

This is based an answer from Mr.Wizard: Subsets of a list.

answered Feb 09 '21 at 17:10

Ferca

494
3
8

Thank you. I would like to get a mathematical analysis method using function GeneratingFunction to solve this problem. – A little mouse on the pampas Feb 09 '21 at 17:22
3

@Alittlemouseonthepampas What do you mean by that? It is not fair to add requirements to your question if you had not specified them in the original post. This kind of "moving target" questions is frowned upon here, since it makes it frustrating for answerer and may render their answers outdated when the question changes. – MarcoB Feb 09 '21 at 22:09
I don't think your result matches the result from the code given by the OP. I think the OP wants the 96 combinations of 7 pairs of letters. – JimB Feb 09 '21 at 22:35

score 2 · Answer 3 · answered Feb 10 '21 at 05:23

This (also) does not directly answer your question about using GeneratingFunction but it is about 2,000 times faster than the original code and does generate all of the arrangements. This code is a bit slower to generate the number of arrangements compared to your answer using SeriesCoefficient.

g[arrangement_, remaining_] := Module[{first, unique, newArrangements, r},
  first = remaining[[1]];
  unique = remaining[[2 ;;]] // DeleteDuplicates;
  newArrangements = Join[arrangement, {{first, #}}] & /@ unique;
  r = (Delete[remaining[[2 ;;]], Position[remaining[[2 ;;]], #, 1, 1][[1, 1]]]) & /@ unique;
  {newArrangements, r}]
(* Initialize arrangements and remaining items to be assigned *)
arrangements = {};
remaining = {a, b, c, c, c, c, d, d, d, d, e, e, e, e};
(* First pair *)
results = g[arrangements, remaining];
arrangements = results[[1]];
remaining = results[[2]];
(* 2nd through 7th pairs *)
Do[
  n = Length[arrangements];
  a2 = {};
  r2 = {};
  Do[results = g[arrangements[[i]], remaining[[i]]];
   a2 = Join[a2, results[[1]]];
   r2 = Join[r2, results[[2]]],
   {i, n}];
  arrangements = a2;
  remaining = r2,
  {j, 2, 7}];
(* Remove duplicates )
t = (Sort[#] & /@ arrangements) // DeleteDuplicates;
Length[t]
( 96 *)

score 1 · Answer 4 · answered Feb 10 '21 at 01:32

1

A feasible method(海洋之心):

set = {a, b, c, d, e};
f = Times @@ 
  DeleteDuplicates[
   Flatten[Table[1/(1 - set[[i]]*set[[j]]), {i, 1, 5}, {j, 1, 5}]]]
SeriesCoefficient[f, {a, 0, 1}, {b, 0, 1}, {c, 0, 4}, {d, 0, 4}, {e, 
  0, 4}]

But I don't understand the specific principle. I hope you can provide more detailed code and explanation.

answered Feb 10 '21 at 01:32

A little mouse on the pampas

5,760
2
13
40

2

That seems to get you the number of unique arrangements (96). But don't you need to generate the actual arrangements? – JimB Feb 10 '21 at 01:53
@JimB Yes, I want to get the final permutation number by pure mathematical method. I don't need the detailed results of each group, just the total number 96. – A little mouse on the pampas Feb 10 '21 at 01:55

How to use function `GeneratingFunction ` to solve this combinatorial problem efficiently?

4 Answers4