compressed = "1:eJzV3VFoVmUYB/\
CzTdtsrVxrLTPZVk5dM5eNESKyCwkRClMvRIYXy1RGmYRGSBci4oWIGIhIF+\
I3diESXoiIFyKyi6joIqK6iIguJKKLiOgiIoJ2nlD6juf891/f/5V/N8L6Pn+u533Oec/\
7nvd93v7XDmzb25Jl2cEFs3+8PHnw0N6DTf/+qTm756e22T+2TRyaPPDWxJuTXbM/TL46+\
0fJZzP5Z6/f/ew/Ks/nny1hlFv5N/ta7JVbdFweqP/3bJVovwcZZQbExUm5ScdlIv/m+\
032yjCduyvzb9bKW9pJuUHHZW3+zU/\
8lYH8s8cY5SOQu07KGrqld4PcdVKu0y39MYiLkzKef/YCozTl31xQnrtOyjU6Lp+\
CuDgpi/LPFjLKHpC7TspOuqU/A3FxUq7QLT2SVfcBTsrqjL1jDmbV/\
bSTsoNu6X0gd52Uy3RLfw5y10kZolu6oz6Ctkpnxo5JvgBxcVKepePSnVWP7Z2Ui3Tufgn\
i4qT0Z+wT/\
GhW3Qc4KdN0XL4GcXFSpmjljay6D3BSLtBK3Ftr5S3tpJynlaX137RVeumr8RuQu07Kioz\
tA/aD3HVSztIt/S2Ii5OyjG7p9vybq8pz10lpzdiR8HcgLk7K+\
owdk2gUFF2N8jaduxoFXQEaJe7s1P1Fo6C7lEbppq9GjYJ6Eo0yQueuRkG9vUbZTeeuRkF\
PZBpl4j4r6KlZowzTLa1R0MhGo/Rk7P1Fo6DRp0aJ2XNq/kWjoBkCjfI4HReNgmZxNMoO+\
mrUKGimTaPErB/Vq2mUOWdDG1a203HRKGjGWqMM1v+eyRX0VkGj5H+\
NG5NoFPTmR6NsoVtao6C3cxrllfusoDeoGiVWgFF9gEZBb7k1ygB9NWoUtBJBo2ymW1qjo\
NUiGuVRuqU1ClrRo1E20XHRKGjVlUZ56T4raGWcRumkW1qjoNWLGmUjHReNglaYapR490n\
dMTUKWgWsUeKJmnqC1yhopbZGWUznrkZBq+\
k1yhiduxoF7XjQKL107moUtCtFo2yg46JRboK4aJR8LxE3ytIoMctY0QdolPV0XDTKDRAX\
jbKMzl2Nsiur7gM0yjo6LholxkC18pbWKA9nbB+gUXrqf+\
sESrxdpfppjTIOWlqjLKVzV6NcA1ejRhmlc1ejxPuHVeUtrVE66NzVKFdBXDTKCB0XjXIl\
uRLzIc33T2mvv1YSKGvpuGiUWPvTl1J5iM5djXIZtLRGGabjolFiDUHF06FG6anPpeRKzP\
dUjEk0StyTqX5ao1wCLa1R2unc1SgXkytDdO5qlHjXWvEspVG66dzVKIPgatQog3RcNMo0\
aGmNkv8XbmyvUaaSKyvpuGiUC8mVLjp3Ncr55MoAHReNErOMtfKrUaNEr0b1ARol3vCjfe\
UNK/H8SfXTGqWrvh0SKJ107mqUmDddnFLpp3NXo8S1UtGraZQ2Onc1ymaQuxqll46LRjmd\
Vd8xNUrkErXaVaOcSq4so+\
OiUU4mV1rp3NUoJ5Irhd0QyZWN4GrUKIX1tMmVuENX3DE1SmFFVnLlKGhpjVJ4p59cOZJc\
KbwVSq70gpbWKIW53+TKYRAXjdJNx0WjxPtwNP/\
SsBJXIzW21yiRWbXyltYohTFCcqW1PrMSKIvo3NUo+0HuapROOi4aZRTkrkbJ/\
9o89s41rOwDcdEo8QRPje01yu7kSuHqSK601LdDAqWDzl2NEndM9KTasFL4PZMr7fW/\
dQKl8FlypRvERaNEP02N7TVK4ZsJlEV0XDRKF4iLRmmmc1ejFH7rBEorHReNEmN71Ac0rM\
T9hZ9naFgZS67E1UH10xol5uTQmESjULmrUUbnikvDSguduxqlkFkJlCY6dzVK91wtrVH4\
frphZWCurJufMpnlX//q3q/PdYvLu6F//jL99cbvzg0rHU2KnmJOhXrKmfP/yETh6y+\
0g7g4KXytmePgmnVSnsjm1d/UylvaSdlDX42Ft+a2yiidu60gd52U/\
XRcjoHcdVL4qogLQVyclGX01RizQqvKc9dJ4WtxtoC4OCmH6ZY+\
CnLXSXmPVppAXJyUMbql2+qz3Fbpo6/G2FtV81firkE9Sx0BueukHKNz96+\
sOnedlOO0ElleMSZxUmIlEzV79SeIi5Nygo5LvgSgak2skxIVjqg75h8gLk4KX2O9sGLVV\
jlFt/TvIC5OymlaiWeUij7ASVmesf107PWtlbe0k8KfvhBVaSr6ACcl1sBT95ffQO46KQN\
0Sx8Gueuk8KeY/Ari4qTE+5pmRinsN7BVztFx+QXExUn5gFbeBbnrpMS+Oer+\
8jOIi5PCn0EVc08VfYCTEjt4qTtm1J6o+Sv8yWfvgNx1UrbQufsTyF0nhT9vr7BbzFbJf+\
BGWT+CuDgpU3RcYgVpRU0VJ2Urnbs/gLg4KdN0XKLaYEUf4KTEGgKqD7gN4uKkxFtnqp+\
Od4qoHrOJsp3O3Vg/0Vfe0k4Kf45yYa+vrcKfdf09yF0n5RIdlwMgd50U/oR1dIamk/\
IhHRd0hqaTMkTnLjpx0km5TMcFnTjppMTJZw2fW+\
mkxJ19AaOgEyedlNV07qITJ52UK3TuohMnnZSddO6i8xmdlKt0XND5jE5KPMVSY3t0PqOT\
co2OCzqf0UkZp3MXnc/opFyn44JOM3RS1mRsH4BOM3RS4t0nNbZHpxk6Kbvo3EWnGTopN+\
jcLVR3slWG6dxFZ/\
85KTfpuOwGLe2kxM50amyPzv5zUm7RcUEn5TkpM3eVfE9PQQHmhjur4rntnne/\
XvIZf8TSGPgfcVI20k1zHlw+TkosiaEG4+tASzspW+d3+\
VRMmDgpQ3Tuvgji4qSM03GJRSkVQ1cnZZiOyyiIi5OyllZiKVTFIMJJ4Tf2joC4OClPZuw\
DaizAq+gDnBR+q3Isiq6Vt7STspSOS+\
GoCFslXm9Rj9zDIHedlKfouJwDueukrKNz9zkQFyeF304ez5Ft5bnrpPDbyYckm9LTK7F4\
m+rVzoLcdVL4DfKDki3/6ZUNdEsXDvqxVXrpqzGyvOavxOZWaiR8BuSuk8IXMRiQlGVIr/\
TRLR3b4irGJE7K0Yy9vzwD4uKk8GUZokevGNs7KXxZhn4QFyeln87dwjFttgpfaKIXxMVJ\
iblm6o4ZG8/\
RjLWJwpfOiNFLrbylnZSn6dzdlFX3AU4KXwxkKchdJ4UvBnIK5K6TcpKOyxIQFyeFL29SO\
GTTVuHLm/SAuDgpm+jcPQly10nhC7Z0g7g4Kcsztg+IO1FFH+Ck8AVbYla6z1/\
hC7Z0gpZ2Us7QuVs4UNhW4UvQPALi4qTwJWjiybhiJOykxCx/M6OgYvJOCl+\
CBpVed1JW0LmLSq87KXxRHVR63Unhi+r01/97tgpfVOcYaGknhS+\
qgwqVOyl8UR1UqNxJ4YvqHAUt7aTwRXVQWW8nJf+BG9u31We5rTJFxwUVwXZS+\
KI6qAi2kzJNxwUVwXZS+KI6qGS0kxLPE1Q/\
jUpGOyl8UR1UMtpJ4YvqoALLTgpfVAcVWHZS+KI6qByxk8IX1UHliJ0UvqhOS/2/\
Z6vwRXVQ8V4nhS+qg4r3Oil8UR1U6tZJ4YvqoFK3TgpfVAcVhnVS+\
KI6qDCsk8IX1UFlVJ0UvqgOKqPqpPBFdW7/TxS+\
qA4qOuqk8EV1UIlOJ4UvqoNKdDopfFEdVNDSSeGL6qCClk4KX1QHFbR0UviiOqigpZPCF9\
VB5R+dFL6oDir/6KTwRXXibW7FmMRJ4YvqoPKPTsrMHeVvgxXDlA==";
Uncompress to get the three lists:
{vsoundAll, decAll, pdivAll} = Uncompress[compressed];
Replicate the issue:
ListLinePlot[{vsoundAll, decAll, pdivAll},
Frame -> True, Joined -> True,
PlotRange -> {{0.01, .4}, {0, 2}},
PlotStyle -> {"DarkColor", "Spahire", Red},
Filling -> {1 -> Top, 3 -> Top, 2 -> {3}}]
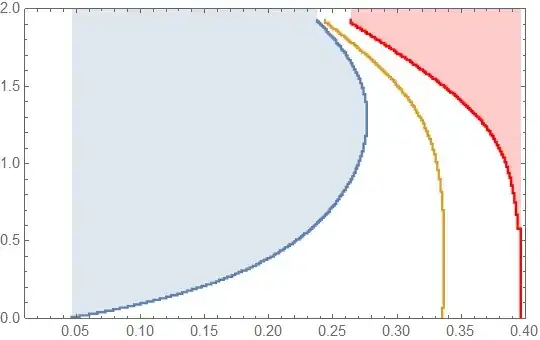
Several ways to fix:
1. Combine the second and third lists as Join[decAll, Reverse@pdivAll] and use it as the fourth input list and add 4 -> Bottom to the Filling option setting:
ListLinePlot[{vsoundAll, decAll, pdivAll, Join[decAll, Reverse@pdivAll]},
Frame -> True, Joined -> True,
PlotRange -> {{0.01, .4}, {0, 2}},
PlotStyle -> {"DarkColor", "Spahire", Red, LineOpacity -> 0},
Filling -> {1 -> Top, 3 -> Top, 4 -> {Bottom, LightGreen}}]

2. Construct a FilledCurve or Polygon using decAll and Reverse @ pdivAll:
ListLinePlot[{vsoundAll, decAll, pdivAll},
Frame -> True, Joined -> True,
PlotRange -> {{0.01, .4}, {0, 2}},
PlotStyle -> {"DarkColor", "Spahire", Red},
Filling -> {1 -> Top, 3 -> Top, 2 -> {3}},
Epilog -> {LightOrange, FilledCurve[Line /@ {decAll, Reverse@pdivAll}]}]

Using
Epilog -> {LightOrange, Polygon[Join[decAll, Reverse@pdivAll]]}
gives the same picture.
3. An alternative approach is to create BSplineFunctions from decAll and pdivAll and plot them using ParametricPlot:
Show[ListLinePlot[{vsoundAll, decAll, pdivAll}, Frame -> True,
PlotRange -> {{0.01, .4}, {0, 2}},
PlotStyle -> {"DarkColor", "Spahire", Red},
Filling -> {1 -> Top, 3 -> Top, 3 -> {2}}],
ParametricPlot[v BSplineFunction[decAll][t] +
(1 - v) BSplineFunction[pdivAll][t],
{t, 0, 1}, {v, 0, 1}, AspectRatio -> 1/GoldenRatio,
PlotStyle -> Green, BoundaryStyle -> None]]






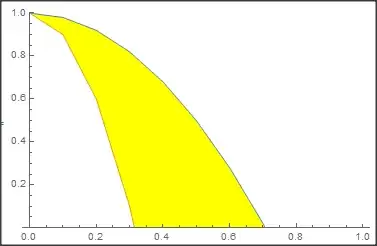
{vsoundAll, decAll, pdivAll}are probably irrelevant here, from a problem-solving-strategy point of view, such assumptions are sometimes the reason problems don't get solved. For instance, this works for me:ListLinePlot[Table[Log[x] + k, {k, 3}, {x, 10}], Frame -> True, PlotRange -> {{1, 10}, {0, 6}}, PlotStyle -> {"DarkColor", "Saphire", Red}, Filling -> {1 -> Top, 3 -> Top, 2 -> {3}}]– Michael E2 Feb 09 '21 at 21:27