Assuming there is a spherical activated carbon particle, the concentration outside the grain is 200 (C[t,ri] == 200), that inside the grain is 0 (Derivative[0, 1][C][t, 0] == 0), the initial condition for PDE is C[0, r] == 0, the radius for the particle is ri(0.001 m). I am new to Mathematica, and when I run this code, the plot shows slight difference with that in MATLAB.
The plot in Mathematica sees a decline of concentration resulting a negative concentration after a period of adsorption, while it remains steady in MATLAB figure. Actually after adsorption equilibrium, the concentration should be stable . Is there a way to fix my code? Thanks.
The concentration becomes negative with growing time:
Figure in MATLAB:
The equation is like this:
Mathematica code:
TT = 3000; ri = 0.001;
sol = NDSolveValue[{D[CC[t, r], t] ==
8*10^-10/r^2*D[r^2*D[CC[t, r], r], r] - 0.01*CC[t, r], CC[0, r] == 0,
CC[t, ri] == 200, Derivative[0, 1][CC][t, 0] == 0}, CC, {t, 0, TT}, {r, 0, ri, ri/50}]
Table[Plot3D[sol[t, x], {x, 0, ri}, {t, 0, VT}, PlotRange -> Full,
ViewPoint -> {-5, -2, 3}], {VT, 100, TT, TT/5}]
This is my MATLAB code:
function test
global c0;
c0=200;
tc=1200;
ri=0.001;
dx=70;
x=linspace(0,ri,dx);
dtL=25;dtR=10;
t=[linspace(0,tc/4,dtL) linspace(tc/4+1,2000000,dtR)];
m=2;
sol=pdepe(m,@mpde,@mpic,@mpbc,x,t);
c=sol(:,:,1);
figure(1);
fig1=surf(x,t,c);
xlabel(' x');
ylabel(' t');
end
function [c,f,s]=mpde(x,t,u,du)
c=1;
f=du8.3E-10;
s=-0.01u;
end
function [pl,ql,pr,qr]=mpbc(xl,ul,xr,ur,t)
global c0;
pl=0;
ql=1;
pr=ur-c0;
qr=0;
end
function u0=mpic(x)
u0=0;
end
Update 2.21:
Some results actually confused me that,
the stable value for
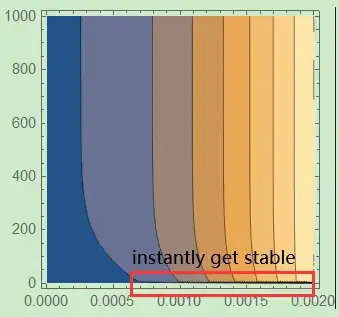
r = 0in MATLAB is around43, while it is22in Mathematica.a gradually increasing could be seen in initial
100seconds, while it instantly reaches stable in Mathematica.
Does this discrepancy result from the difference between MATLAB and Mathematica or the code itself?
T2 = 1000;
sol = NDSolveValue[{D[CC[r, t], t] ==
8.3 10^-10/r^2*D[r^2*D[CC[r, t], r], r] - 0.01 CC[r, t], CC[r, 0] == 0,
CC[ri, t] == 200, Derivative[1, 0][CC][0, t] == 0},CC, {t, 0, T2}, {r, 0, ri, ri/50},
Method -> {"MethodOfLines",
"DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}}]
Table[Plot3D[sol[x, t], {x, 0, ri}, {t, 0, VT2}, PlotRange -> All,
ColorFunction -> ColorData["BlueGreenYellow"], PlotPoints -> 100,
PlotLegends -> BarLegend[Automatic, LegendMarkerSize -> {10, 200}], TicksStyle -> 13,
ViewPoint -> {-3, -2, 1}, AxesLabel -> {"r", "t", "z"}], {VT2, 100, T2, T2/3}]
ContourPlot[sol[r, t], {r, 0, ri}, {t, 0, T2}]


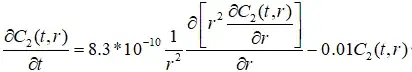


Derivative[0,1][CC][t,ri/50]==0to avoid the removable singularity. With this b.c., the output is consistent with that of MATLAB. Also, why do you type{r,0,ri,ri/50}? This syntax isn't documented and colored red in the notebook. ThoughNDSolvestill (surprisingly) gives a result, the mysterious syntax clearly causes certain problem. – xzczd Feb 21 '21 at 09:11Derivative[0,1][CC][t,ri/50]==0, and remove,ri/50. The result displays thatNDSolveValue::bcedge: Boundary condition (CC^(0,1))[t,0.00004]==0 is not specified on a single edge of the boundary of the computational domain.– hithere Feb 21 '21 at 12:00{r, ri/50, ri}. – xzczd Feb 21 '21 at 12:10"DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}}isn't actually necessary here. The real issue turns out to be interesting. See my answer below. – xzczd Feb 22 '21 at 05:49