Trouble iterating my forest fire simulation

Question

I'm having some trouble iterating my simulation of a forest fire. I'm new to Mathematica, so apologies for poor coding. I'm sure there are far neater and more efficient ways of doing this, but I would like to know whats the problem with the method I'm using currently.

This is my code to get the adjacent elements, including wrap around at the boundaries:

neighbourPos[m_, i_, j_] := 
  Transpose[Mod[{i, j} + {{-1, 0, 1, 0}, {0, -1, 0, 1}}, Dimensions[m],]];

In my simulation, 2 represents burning trees, 1 trees and 0 empty ground. After one timestep, trees adjacent to a fire will be set on fire and original fire(s) will burn themselves out and become 0. This my code to simulate the spread of the fire:

nextState[m_] :=  (
  firepos = Position[m, 2]; 
  a = 
    MapAt[2 # &, m, neighbourPos[m, Position[m, 2][[1, 1]], Position[m, 2][[1, 2]]]]; 
  MapAt[0 &, a, firepos])

It seems to work. Up to a point anyway. I would like to eventually plot the thing with ListAnimate. However, when I try to iterate nextState until the fire is burnt out with FixedPointList, it stops working properly after 6 iterations and I get a load of errors.

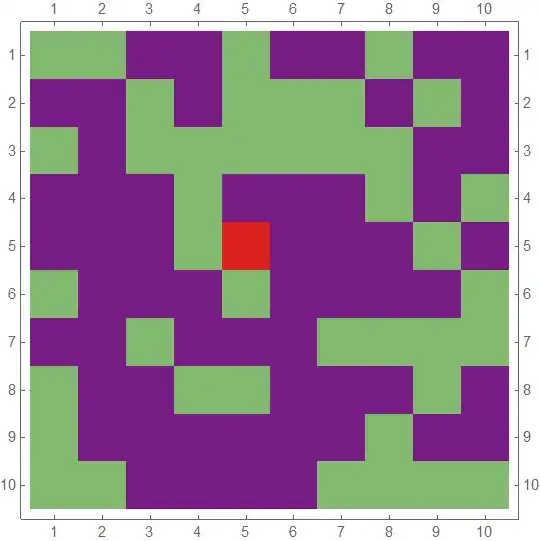
MatrixPlot[mat/2, 
  PlotRange -> {0, 1}, 
  ColorFunction -> "Rainbow", 
  ColorFunctionScaling -> False]

Gives

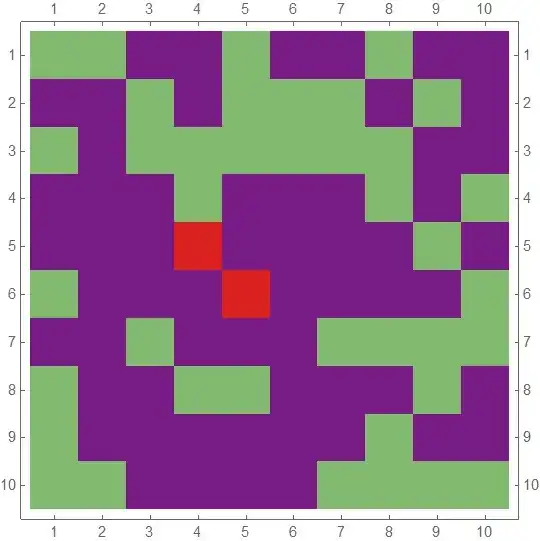
Then

MatrixPlot[nextState[mat]/2, 
  PlotRange -> {0, 1}, 
  ColorFunction -> "Rainbow",  
  ColorFunctionScaling -> False]

But then errors come after more iterations.

fireStates[m_] := FixedPointList[nextState, m];
frames = fireStates[mat];

During evaluation of In[14]:= Part::partw: Part 1 of {} does not exist.
During evaluation of In[14]:= Part::partw: Part 1 of {} does not exist.
During evaluation of In[14]:= MapAt::pkspec1: The expression Mod[1+{}[[1,1]],10,1] cannot be used as a part specification.
During evaluation of In[14]:= Thread::tdlen: Objects of unequal length in Mod[{{0,1,2,1},{1,0,1,2}},{3},1] cannot be combined.
During evaluation of In[14]:= MapAt::psl: Position specification Transpose[Mod[{{0,1,2,1},{1,0,1,2}},{3},1]] in MapAt[2 #1&,MapAt[2 #1&,<<1>>,{{Mod[-1+{}[[1,1]],10,1],Mod[{}[[1,2]],10,1]},{<<1>>,Mod[<<1>>]},<<1>>,{Mod[{}[[1,1]],10,1],Mod[1+{}[[1,2]],10,1]}}],Transpose[Mod[{{0,1,2,1},{1,0,1,2}},{3},1]]] is not a machine-sized integer or a list of machine-sized integers.
During evaluation of In[14]:= MapAt::partw: Part {3,4,2,1,2,3} of MapAt[2 #1&,MapAt[2 #1&,<<1>>,{{Mod[-1+{}[[1,1]],10,1],Mod[{}[[1,2]],10,1]},{<<1>>,Mod[<<1>>]},<<1>>,{Mod[{}[[1,1]],10,1],Mod[1+{}[[1,2]],10,1]}}],Transpose[Mod[{{0,1,2,1},{1,0,1,2}},{3},1]]] does not exist.
During evaluation of In[14]:= Thread::tdlen: Objects of unequal length in Mod[{{1,2,3,2},{1,0,1,2}},{3},1] cannot be combined.
During evaluation of In[14]:= MapAt::psl: Position specification Transpose[Mod[{{1,2,3,2},{1,0,1,2}},{3},1]] in MapAt[2 #1&,MapAt[0&,MapAt[2 #1&,MapAt[<<1>>],Transpose[Mod[<<1>>]]],{{1,1,1},{3,1,2,1,3},{3,2,2,1,2,3},{3,3,2,1,3},{3,4,2,1,2,3}}],Transpose[Mod[{{1,2,3,2},{1,0,1,2}},{3},1]]] is not a machine-sized integer or a list of machine-sized integers.
During evaluation of In[14]:= MapAt::partw: Part {2,2,3,4,2,1,2,3} of MapAt[2 #1&,MapAt[0&,MapAt[2 #1&,MapAt[<<1>>],Transpose[Mod[<<1>>]]],{{1,1,1},{3,1,2,1,3},{3,2,2,1,2,3},{3,3,2,1,3},{3,4,2,1,2,3}}],Transpose[Mod[{{1,2,3,2},{1,0,1,2}},{3},1]]] does not exist.
During evaluation of In[14]:= Thread::tdlen: Objects of unequal length in Mod[{{1,2,3,2},{1,0,1,2}},{3},1] cannot be combined.
During evaluation of In[14]:= General::stop: Further output of Thread::tdlen will be suppressed during this calculation.
...

Answer 1

I found your simulation idea interesting, so I decided to look into the problem. What I found was that your implementation of nextState is mostly where the fault lies. It simply does not do what it name advertises — it does not compute the next state of the simulated world. Here is the code I used to develop a working simulation. I use a more modular approach than yours, because it mad debugging easier.

incombustible = 0;
combustible = 1;
burning = 2;
dim = {10, 10};
SeedRandom[42]
world = RandomChoice[{.5, .5} -> {incombustible, combustible}, dim];
plotMaker[state_] :=
  MatrixPlot[state,
    ColorRules -> 
      {incombustible -> Darker[Brown, .3],
       combustible -> Darker[Green, .4],
       burning -> Red}]

With this last function we can see what our world looks like.

plotMaker[world]

Your neighbourPos function is fine, but it doesn't need to given the whole simuaton state and I thought it would be easier to use if the indices were given to it as a list.

neighbourPos[{i_, j_}] := Transpose[Mod[{i, j} + {{-1, 0, 1, 0}, {0, -1, 0, 1}}, dim, 1]];

Now here is the code you really need to study. Note that finding the von Neumann neighbors of a burning patch is more complicated than you thought is was. Also, note that you have to select the neighbors that are combustible.

nextState[state_] :=
  Module[{nxt, fires, neighbors, inflammable},
    nxt = state;
    fires = Position[nxt, 2];
    neighbors = Union @ Catenate[neighbourPos /@ fires];
    inflammable = Select[neighbors, Extract[nxt, #] == combustible &];
    nxt = MapAt[incombustible &, nxt, fires];
    MapAt[burning &, nxt, inflammable]]

The simulation function I wrote follows your approach, but I insist on giving it a guard to prevent indefinite looping.

simF[init_, max_] := FixedPointList[nextState, init, max]

Now let's look at a simple case where the fire can't burn for long.

initialState = world;
initialState[[6, 5]] = 2;
history = simF[initialState, 5];
Column[plotMaker /@ history]

And here is the initial phase of much more dangerous fire.

initialState = world;
initialState[[10, 5]] = 2;
history = simF[initialState, 6];
Column[plotMaker /@ history]