How to create random isolated clusters periodically?

Question

Let's assume we have a $n \times n$ grid repeated periodically, and I want to create some random isolated patches on it (and assign some value to those grid points).

For a simple example consider this - a grid of RandomPolygon

a = 4; l = 3;
d = 0.1;
w = a*l;
polys = Flatten[ Table[RandomPolygon["Convex",
        DataRange -> {{i+d, i + 1-d}, {j+d, j + 1-d}} a],{i, l}, {j, l}], 1];
Show[Table[MeshRegion[TransformedRegion[polys[[n]], 
     TranslationTransform[{iw, jw}]], MeshCellStyle -> {1 -> Black,
     2 -> {Opacity[0.5], ColorData[112, n]}}], {n, l*l},
 {i, -1/2, 1/2}, {j, -1/2, 1/2}], PlotRange -> {{0, 1}, {0, 1}} w,
 GridLines -> {Range[w], Range[w]}]

Now one can extract the grid points from each regions. However this process is not exactly random.

How to make this regions distributed randomly over the grid?

The number of clusters (and if possible the area covered) should be user defined and the configuration must satisfy periodic boundary condition.

Are there any restrictions on the form of the clusters? And are they allowed to touch at one point as in your example? — Daniel Huber, Feb 14 '21 at 14:41
No, they must be isolated. I have added a small margin d now. — Sumit, Feb 14 '21 at 14:46
Should the region have approx. the same are like in your example or should they differ? — Daniel Huber, Feb 14 '21 at 18:00
not necessary - actually more diverse shape is better. Only restriction I want to put is on total area. — Sumit, Feb 15 '21 at 10:53

Sumit · Accepted Answer · 2021-02-15T11:46:58.040

One way can be by Generating a Periodic Voronoi Mesh.

Adopting @ChipHarst's answer we can start by generating a periodic Voronoi Mesh.

pts = RandomReal[{-1, 1}, {8, 2}]; 
pts2 = Flatten[Table[TranslationTransform[{2 i,2 j}][pts],{i,-1,1}, {j,-1,1}],2];
vor = VoronoiMesh[pts2, 2 {{-1, 1}, {-1, 1}}];
vcells = Catenate[NearestMeshCells[{vor, 2}, #] & /@ pts];
pvor = MeshRegion[MeshCoordinates[vor], MeshCells[vor, vcells]];
pts = RandomPoint[#, Round[200*Area[#]/4]] & /@ MeshPrimitives[pvor, 2];
pts = Map[If[Abs[#] > 1, Sign[#] (Abs[#] - 2), #] &, pts, {3}];
Show[Table[MeshRegion[TransformedRegion[pvor, TranslationTransform[{2 i, 2 j}]], 
  MeshCellStyle -> {1 -> Black, 2 -> None}], {i, -1, 1}, {j, -1, 1}],
  Graphics[{Line[{{-1, -1}, {1, -1}, {1, 1}, {-1, 1}, {-1, -1}}], 
  {ColorData["Rainbow", #/8], PointSize[Medium], Point[pts[[#]]]} & /@ Range[8]}], 
  PlotRange -> {{-1, 1}, {-1, 1}} 1.01]

The selected points can be mapped on the grid

l = 10;
pts = Map[Union, Round[l*pts]];

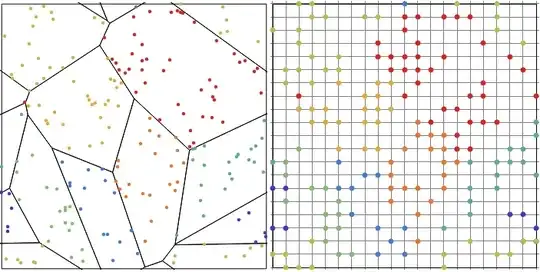
However in this way the final number of points can be significantly reduced and it does not exactly look like clusters.

RandomSample for existing grid

l = 10 (*grid range*)
pts = Flatten[Table[{i, j}, {i, -1.5, 1.5, 1/l}, {j, -1.5, 1.5, 1/l}], 1];
pts = Table[Select[pts, RegionMember[r, #] &], {r, MeshPrimitives[pvor, 2]}];
pts = Map[If[# > 1 || # <= -1, Sign[#] (Abs[#] - 2), #] &, pts, {3}];
pts1 = RandomSample[l*#, Round[0.7*Length[#]]] & /@ pts;
(*for 70% coverage with scale l*)
Show[Table[MeshRegion[TransformedRegion[pvor, TranslationTransform[{2i,2j}]], 
 MeshCellStyle->{1->Black, 2->None}], {i,-1,1}, {j,-1,1}],
 Graphics[{Line[{{-1,-1},{1,-1},{1,1},{-1,1},{-1,-1}}], {ColorData["Rainbow", #/8],
 PointSize[Medium], Point[pts[[#]]]} & /@ Range[8]}],
 PlotRange -> {{-1, 1}, {-1, 1}} 1.01]
Show[ListPlot[pts1, PlotStyle -> Table[{PointSize[Large],
 ColorData["Rainbow", i/8]}, {i, 8}]], ListPlot[l pts, 
 PlotStyle -> Table[{PointSize[Small], ColorData["Rainbow", i/8]}, {i, 8}]],
 Frame -> True, PlotRange -> {{-l, l + 1}, {-l, l + 1}},  PlotRangePadding -> 0,
 GridLines -> {Range[-l+1,l], Range[-l+1,l]}, AspectRatio -> 1]

How to create random isolated clusters periodically?

1 Answers1