how to successively plot Community Graphs by iteratively using VertexDelete[]

Question

Given the matrix wam:

wam={
 {∞, ∞, ∞, ∞, ∞,   ∞,  0.180744, ∞, ∞, ∞, ∞,  ∞, 0.196146, ∞, ∞, 0.192559}, 
 {∞, ∞, 0.199743, 0.189167, ∞, 0.177828, 0.136293, 0.198179, 
   0.170862, ∞, ∞, 0.150103, 0.152068, ∞, 0.145293, 0.147801}, 
 {∞, 0.17492, ∞, ∞, ∞, ∞,  ∞, 0.196928, ∞, 0.18818, ∞, ∞, ∞, ∞,  ∞, ∞}, 
 {∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {0.164114, 0.189904, ∞, ∞, ∞, 0.142879, ∞, 0.173485, ∞, 0.195519, ∞,
     0.179716, 0.152131, ∞, ∞, 0.197488}, 
 {0.193476, 0.186542, ∞, 0.196847, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, 
     0.184613, ∞, 0.195341, 0.190637}, 
 {∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {0.17967, ∞, ∞, ∞, ∞, 0.165566, ∞, ∞, ∞, ∞, ∞, ∞, 0.16862, ∞, ∞, ∞}, 
 {∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞},
 {∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {∞, ∞, ∞, ∞, ∞, 0.183951, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {∞, ∞, ∞, ∞, ∞, 0.189936, 0.16593, 0.197014, ∞, ∞, ∞, 0.194794, ∞, ∞, ∞, ∞}, 
 {0.189579, 0.167198, ∞, ∞, ∞,  0.18947, ∞, ∞, ∞, 0.187049, ∞, ∞, ∞, ∞, ∞, ∞}, 
 {∞, 0.149854, ∞, ∞, ∞, 0.188494, 0.150641, 0.192737, 0.194964, ∞, ∞, ∞, 
   0.14314, 0.15716, 0.14968, ∞}
};

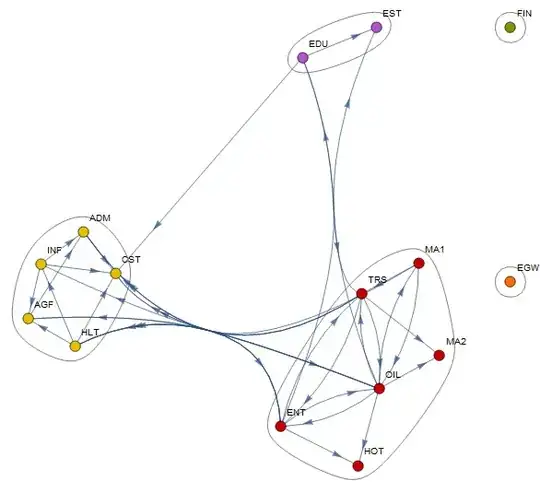
I generate the directed graph and its community structure:

 vnames = {"AGF", "OIL", "MA1", "MA2", "EGW", "CST", "WHS", "TRS", 
      "HOT", "INF", "FIN", "EST", "ADM", "EDU", "HLT", "ENT"};
 wag = WeightedAdjacencyGraph[vnames, wam, VertexLabels -> "Name", 
     ImageSize -> 250]
 CommunityGraphPlot[wag, FindGraphCommunities[wag]]

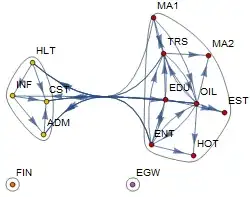
Then I delete a vertex from the graph wag and find the communities in the resulting graph:

vdwag = VertexDelete[wag, {"WHS"}]
FindGraphCommunities[vdwag]
 (* {{"OIL", "MA1", "MA2", "TRS", "HOT", "EST", "EDU", "HLT", 
     "ENT"}, {"AGF", "CST", "INF", "ADM"}, {"EGW"}, {"FIN"}} *)

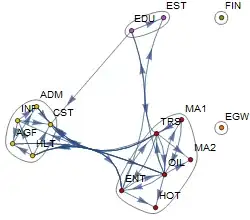
Then I wanted to draw the communities using:

 CommunityGraphPlot[vdwag, FindGraphCommunities[vdwag]]

However, this does not work, although vdwag is a graph. WHY?

It works here. What version of Mathematica do you have? Until very recently, VertexDelete / EdgeDelete have been so buggy as to be completely unusable. Yes, fundamental functions like these were unusably buggy. If you have anything before v12.0, I'd say forget about any reliability when working with Graph. Ideally, use 12.2. — Szabolcs, Feb 14 '21 at 16:56
In version 11.3.0, EdgeWeights are not properly modified byVertexDelete. A workaround: use EdgeDelete, that is, try edwag = EdgeDelete[wag, DirectedEdge["WHS", _] | DirectedEdge[_, "WHS"]] — kglr, Feb 14 '21 at 17:05
@Szabolcs: I have Mathematica version 11.3. Very discouraging bug. — Tugrul Temel, Feb 14 '21 at 17:06
@kglr: Does this mean that I have to write a long statement to achieve my goal because I have around 16 vertices to delete? I am afraid yes. Thanks. — Tugrul Temel, Feb 14 '21 at 17:10
My package, IGraph/M, has IGWeightedVertexDelete which can handle weighted graphs properly in v11.3 as well. But it will discard all edge properties except weights. There is also IGTakeSubgraph, which handles all properties correctly in versions prior to 12.0 as well, but it is very slow. — Szabolcs, Feb 14 '21 at 17:21
Also consider IGWeightedAdjacencyGraph and IGWeightedAdjacencyMatrix which are actually consistent with each other in the handling of zeros and infinities, unlike the builtin WeightedAdjacencyMatrix and WeightedAdjacencyGraph. — Szabolcs, Feb 14 '21 at 17:22
Finally, IGraph/M has a bunch of properly documented community detection methods. If you ever want to publish this work in a paper, the referee will ask you: what method did you use to find communities? And all you can say "I used Mathematica, I don't know how it works." If you ask Wolfram, they will not give a satisfactory answer about FindGraphCommunities — Szabolcs, Feb 14 '21 at 17:25
@Szabolcs: Thank you for the detailed comment and suggestions. I tried IGWeightedVertexDelete[wag, {"WHS"}, VertexLabels -> "Name"] and it works as I expect it. The resulting directed graph seems to be identical to one @kglr presented. For now, I solved the problem with by @kglr's answer and also by IGraph. Thanks to you. and @kglr. — Tugrul Temel, Feb 14 '21 at 17:37
@kglr: In editing the matrix wam how did you insert Infinity sign? If I had known how to do it, I would have used the mathematical sign when posting the question. Maybe you have a special program for it. — Tugrul Temel, Feb 14 '21 at 18:26
Tugrul, I use the browser extension mathematica editor buttons for stack exchange — kglr, Feb 14 '21 at 18:34

kglr · Accepted Answer · 2021-02-14T18:06:52.607

In versions prior to 12.+, due to a bug in VertexDelete, (among other things) EdgeWeights are not properly updated:

PropertyValue[vdwag, EdgeWeight] == PropertyValue[wag, EdgeWeight]

True

$Version

"11.3.0 for Microsoft Windows (64-bit) (March 7, 2018)"

A work-around: use EdgeDelete + VertexDelete:

edwag =  VertexDelete[EdgeDelete[wag, IncidenceList[wag, "WHS"]], "WHS"];
{VertexList[vdwag], EdgeList[vdwag]} == 
  {VertexList[edwag], EdgeList[edwag]}

True

CommunityGraphPlot[edwag, FindGraphCommunities[edwag]]

EdgeDelete has a similar issue.

If none of the vertices is a List we can use the following two functions instead of VertexDelete and EdgeDelete:

ClearAll[vertexDelete, edgeDelete]
vertexDelete = VertexDelete[EdgeDelete[#, IncidenceList[#, #2]], #2] &;
edgeDelete = vertexDelete[#, VertexList@Flatten[{#2}]] &;

Examples:

CommunityGraphPlot@vertexDelete[wag, "WHS"]

CommunityGraphPlot@vertexDelete[wag, {"WHS", "OIL"}]

CommunityGraphPlot@edgeDelete[wag, "AGF" \[DirectedEdge] "WHS"]

CommunityGraphPlot@edgeDelete[wag, 
 {"AGF" \[DirectedEdge] "WHS", "MA1" \[DirectedEdge] "OIL"}]

how to successively plot Community Graphs by iteratively using VertexDelete[]

1 Answers1