Suppose we have a real function $f:\mathbb R^2 \rightarrow \mathbb R$ and we would like to know if this function factorizes into $f(x,y)=f_1(x)f_2(y)$ for some real functions $f_1,f_2$. Is there an easy way of doing this in mathematica ? The program would return a set $f_1,f_2$ that does the job if they exist and would say it is not possible if such $f_1,f_2$ do not exist. I've been playing around with the "Collect" command, but I haven't figured out a way to get what I want.
Example: $f(x,y)=xy^2 - 4y^2 - xy+4y+x-4$ can be factorized into $(x-4)(y^2-y+1)$, so the program would return $f_1(x)=x-4, f_2(y)=y^2-y+1$. But $f(x,y) = xy+1$ cannot be factorized, so it would return impossible.
EDIT: I do not suppose that $f$ is separable, I would like to find out if it is, and in that case, get the factors $f_1,f_2$.
EDIT2: If I want to check the separability of a function using the proposed technique below, here is what I get:
Let's take a function that is NOT seperable:
ftest[t_, s_] := (s (t - T[1]) (s t - t T[1] + (T[1] - T[2]) T[2]))/Sqrt[s t (s - T[1]) (t - T[1]) (s - T[2]) (t - T[2]) (s - T[1] + T[2]) (t - T[1] +T[2])]
Checking separability using the proposed code by taking the product of $f_1$ by $f_2$:
Simplify[getGX[ftest[x, y], x, y]*getHY[ftest[x, y], x, y] - ftest[x, y]] == 0
This returns true, although ftest is not separable.
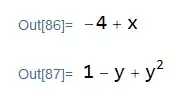


getGXevaluated (does not return withHeadthe same asgetGX). – Michael E2 Feb 16 '21 at 17:32With[{gx = getGX[ftest[x, y], x, y]}, FreeQ[gx, getGX] && Simplify[gx*getHY[ftest[x, y], x, y] - ftest[x, y]] == 0]returnsFalse. (Check the result ofgetGX.) – Michael E2 Feb 16 '21 at 18:47